5. Мінімізація булевих функцій
Импликантой функції називають деяку логічну функцію, яка звертається в нуль на тому ж наборі змінних, на якому дорівнює нулю сама функція.
Будь кон'юнктивний терм (елементарна кон'юнкція) або група термів, з'єднаних знаками диз'юнкції, що входять до СДНФ, є импликантами вихідної функції
Елементарна кон'юнкція (кон'юнктивний терм), в якій видалений один або кілька первинних термів, називається простий импликантой.
Методів мінімізації булевих функцій в даний час існує досить багато. Всі вони, як правило, складаються з двох етапів. На першому етапі отримують список всіх простих импликант, тобто скорочену ДНФ. На другому етапі, використовуючи таблицю покриттів, видаляють "зайві" імпліканти, покривемие іншими импликантами. В результаті отримують ДНФ, з якої не можна видалити жодної імпліканти. Таку ДНФ називають тупиковою.
5.1 Метод Квайна
На першому етапі в методі Квайна попарно порівнюють все імпліканти, що входять до СДНФ, з метою виявлення можливості поглинання якоїсь змінної на основі закону склеювання:
.
Процедура триває до тих пір, поки не залишиться жодного члена, що допускає поглинання з іншим термо. В результаті отримують кілька простих импликант. Диз'юнкція цих импликант є скороченою ДНФ.
На другому етапі будується таблиця покритій.В рядках цієї таблиці зазначають знайдені прості імпліканти, а в стовпчиках - терми вихідного вираження функції. Клітини таблиці відзначаються, якщо проста импликанта входить до складу будь-якого терма. В результаті мінімізація булевої функції зводиться до того, щоб знайти таку мінімальну кількість простих импликант, які покривають всі стовпці. В результаті отримують тупикову ДНФ.
Недолік методу-необхідність попарного порівнянні всіх кон'юнктивні термів на першому етапі при знаходженні простих импликант. З ростом числа вихідних термів збільшується кількість попарних порівнянь, що ускладнює вирішення завдання мінімізації.
5.2 Метод Квайна із застосуванням п-мірних кубів
Даний метод усуває недолік попереднього методу, тобто усуває необхідність попарного порівняння всіх термів на першому етапі при знаходженні простих импликант. Для цього будується п-мірний куб, по якому візуально можна визначити ті кон'юнктівние терми, склеювання яких породжують прості імпліканти.
При вирішенні задачі мінімізації булевої функції зручно замість кон'юнктивні термів використовувати, відповідні їм, виконавчі набори.
Мінімізувати булеву функцію
.
Тут в дужках стоять десяткові еквіваленти відповідних двійкових наборів.
Уявімо функцію у вигляді СДНФ:
Запишемо кон'юнктівние терми у вигляді двійкових наборів:
.
Побудуємо одиничний 4 - мірний куб і виділимо вершини, відповідні двійковим набором, що входять в задану булеву функцію (рис. 10):
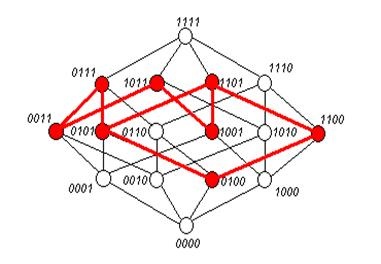
1 етап. Визначення скороченою ДНФ.
Застосуємо закон склеювання для зазначених вершин (для двійкових наборів) куба, з'єднаних ребром:
Прочерк означає, що змінна в цьому місці відсутня.
Для деяких простих импликант склеювання можна продовжити:
Згідно із законом ідемпотентності:
Диз'юнкція отриманих простих импликант є скороченою ДНФ:
2 етап. Визначення тупикової ДНФ.
Для визначення тупикової ДНФ побудуємо таблицю покриттів, в яку слід включати і виконавчі набори, які не брали участі в склеюванні:
Визначаючи мінімальну кількість рядків, що покривають всі стовпці таблиці, знаходимо тупикову ДНФ:
Недоліком методу є сама побудова п - мірного куба, тому що при числі змінних це побудова важко.
5.3 Метод Квайна - Мак-Класки
Метод Квайна - Мак-Класки є попередній метод, але без геометричної побудови п - мірних кубів: куби присутні, але абстрактно.
Метод заснований на кубічному поданні кон'юнктивні термів ДНФ з попередніми розбиттям кубів на підгрупи, що визначаються однаковим числом одиниць. Розбиття дає можливість порівнювати куби тільки сусідніх по числу одиниць груп для зменшення кількості переборовши.
У итеративной процедурі мінімізації попарне порівняння можна робити тільки між сусідніми групами.
Знаходження простих імплікат на першому етапі:
1. Всі вихідні кон'юнктівние терми записуються у вигляді їх довічних наборів.
2. Всі набори розбиваються на непересічні групи по числу одиниць. Умова освіти r-куба - наявність розбіжності в (r-1) -куб тільки по одній координаті в одному двійковому розряді і наявність загальних незалежних координат.
3. В i-групу включають всі виконавчі набори, що мають в своєму записі i одиниць.
4. Попарне порівняння проводиться тільки між сусідніми по номеру групами. Групи, які розрізняються в двох розрядах і більше, не має сенсу порівнювати.
Мінімізувати булеву функцію
Інформація про роботу «Математична логіка»
Розділ: Математика
Кількість знаків з пробілами: 29947
Кількість таблиць: 14
Кількість зображень: 9
стверджують або заперечують будь-які відносини між об'єктами і явищами реальної дійсності. 3.Математіческая логіка і «Здоровий глузд» в XXI столітті. Логіка - не тільки суто математична, але також і філософська наука. У XX столітті ці дві взаємопов'язані іпостасі логіки виявилися розведеними в різні боки. З одного боку логіка розуміється як наука про закони правильного мислення.
цікавості. Вправи однотипні. Тому просто необхідно доповнювати дані в підручнику вправи додатковими завданнями розвивального характеру. Глава II. Методика вивчення елементів алгебри і математичної логіки. § 1. Методика вивчення числових виразів, виразів зі змінними, числових рівностей і нерівностей, рівнянь. Вивчення числових виразів, рівностей і нерівностей, а.
твердження "Я ніколи не користуюся методами математичної логіки". Очевидно, що вони суперечать один одному, проте вони цілком можуть виявитися одночасно хибними. Наприклад, якщо ви фахівець з математичної логіки, то ви повинні часто користуватися її методами, але навряд чи вони потрібні вам кожен день вашого життя. Закон виключеного третього призначений для використання в галузі точних наук.
постулати D (тобто аксіоми Ax # 204; F # 205; A * і дедуктивні засоби P # 204; Fn + 1), то говорять про побудову теорії як формальної системи F.S. =