Завдання мінімізації булевої функції полягає в тому, щоб знайти еквівалентну їй формулу, що має мінімальну складність. Під складністю формули розуміють кількість вхідних в неї букв. Найбільш добре розроблені методи мінімізації Бєлєва функцій, представлених в ДНФ. Ці методи засновані на понятті простий імпліканти.
Якщо деяка булева функція # 966; дорівнює нулю на тих же наборах, на яких дорівнює нулю інша функція F. а також і на деяких інших наборах, то кажуть, що функція # 966; входить в функцію F і є її импликантой. Умова входження записується в такий спосіб: jÌF. Наприклад, розглянемо функцію F = XÅY. Її импликантами є функції
Простими импликантами булевої функції F називають такі елементарні кон'юнкції, які самі входять в дану функцію, але ніяка власна частина цих кон'юнкція в функцію F не входить. Власної частиною називають твір, отримане шляхом виключення з даного твору одного або декількох співмножників. Наприклад, твір має такі власні частини:
Наприклад, для Значить і є простими импликантами функції F.
Прості імпліканти є найкоротші елементарні кон'юнкції, що входять в дану булеву функцію.
Будь-яка булева функція може бути представлена у вигляді диз'юнкції всіх своїх простих импликант. Диз'юнкція всіх простих импликант називається скороченою ДНФ булевої функції. Існують різні алгоритми отримання скороченою ДНФ булевої функції. Одним з найбільш добре розроблених є метод Квайна.
Метод Квайна. Цей метод заснований на перетворенні СДНФ за допомогою операції неповного склеювання і поглинання.
Операція склеювання (повного) визначається співвідношенням
Кажуть, що два члени XY і склеюються по змінної Y.
Операція неповного склеювання визначається формулою
У правій частині крім члена X. виходить в результаті склеювання, записуються обидва члени, які беруть участь в склеюванні.
Операція поглинання визначається співвідношенням
Теорема Квайна. Якщо в СДНФ булевої функції провести всі операції неповного склеювання, а потім всі операції поглинання, то вийде скорочена ДНФ цієї функції, тобто диз'юнкція всіх її простих импликант.
Практично скорочену ДНФ зручно знаходити в такій послідовності.
Провести в СДНФ всі можливі операції неповного склеювання констітуєнт одиниці і всі можливі операції поглинання.
Потім провести всі можливі операції неповного склеювання і поглинання членів з (n -1) буквою.
Провести всі можливі операції неповного склеювання і поглинання членів з числом букв, рівним (n -2) і т. Д.
Проводимо всі можливі операції неповного склеювання і поглинання з чотирибуквеними кон'юнкції. Результат вносимо в таблицю:
Номери склеюються Результат
Записуємо скорочену формулу, в яку повинні увійти кон'юнкції, отримані в результаті склеювання, і ті вихідні констітуенти одиниці, що не склеїлися:
В отриманому виразі виконуємо знову всі можливі операції склеювання і поглинання:
Перший і четвертий, другий і третій члени попарно склеюються. П'ятий і шостий члени залишаються. Таким чином, отримаємо:
У цьому виразі немає членів, які склеюються, тому воно є скороченою диз'юнктивній нормальною формою. Для того, щоб знайти мінімальну діз'юнктівную форму, можна скористатися импликантной матрицею. У импликантной матриці стовпці позначаються констітуентамі одиниці заданої функції, а рядки - импликантами, отриманими в результаті склеювання (табл. 5).
Якщо импликанта є власною частиною деякої констітуенти одиниці, то клітина матриці, що відповідає цій импликанте і конституенте одиниці, позначається хрестиком. Щоб отримати мінімальну діз'юнктівную нормальну форму заданої функції, потрібно знайти мінімальне число импликант, які спільно накривають хрестиками всі колонки импликантной матриці. У наведеному прикладі мінімальна діз'юнктівная форма заданої функції має вигляд
.
Може виявитися, що функція має кілька різних мінімальних форм однакової складності.
Карти Карно (Вейча). Карта Карно являє собою прямокутник, розділений на клітини, кількість яких дорівнює кількості всіх можливих наборів незалежних змінних заданої логічної функції. Для функції двох змінних карта містить 4 клітини, для функції 3 змінних - 8 клітин і т.д.
Розглянемо карту для двох змінних (рис. 21). Кожна клітина карти відповідає конституенте одиниці.
Мал. 21. Карта Карно для Рис. 22. Карта Карно для
функції 2-х змінних функції 3-х змінних
З додаванням змінної карта подвоюється. На рис. 22 показана карта Карно для функції 3 змінних.
При побудові карти можна користуватися таким правилом: карта Карно для функції n змінних виходить з карти для функції n -1 змінних, якщо останню подвоїти шляхом додавання до неї точно такий же, розташованої симетрично відносно довгою межі. При цьому одна половина нової карти позначається новою буквою в позитивної формі, а друга половина - тієї ж буквою, але з запереченням. На рис. 23 показана карта Карно для функції 4-х змінних, отриманої з карти, зображеної на рис. 22. У правильно розміченій карті будь-які дві поруч розташовані клітини відповідають
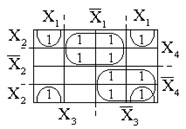
склеювати конституентов одиниці. Крім того, будь-які дві клітини, розташовані по краях карти симетрично зліва і справа, або вгорі і внизу, теж відповідають склеювати конституентов одиниці.
Мінімізація заданої логічної функції за допомогою карти Карно проводиться в такій послідовності.
1. Задана функція перетворюється в СДНФ.
2. Кожна конституента одиниці заданої функції відзначається одиницею у відповідній клітинці карти Карно.
3. Одиниці, розташовані поруч, або симетрично на краях карти, покриваються правильними прямокутниками. При цьому виконуються наступні вимоги:
- число одиниць, що покриваються одним прямокутником, має дорівнювати 2 k. гдеk - ціле число;
- кожен прямокутник повинен покривати як можна більше одиниць, а кількість покривають прямокутників має бути якомога менше;
- одна і та ж одиниця може бути покрита кілька разів різними прямокутниками.
4. Для кожного прямокутника, що покриває одиниці, записуємо кон'юнкцію, в яку повинні увійти букви, які є загальними для одиниць, накритих цим прямокутником.
5. Записуємо мінімальну ДНФ. в яку повинні увійти кон'юнкції, які відповідають усім накриває прямокутникам. Якщо в карті виявилися одиниці, які стоять ізольовано від інших, і не покриті ніякими прямокутниками, то в результуючу диз'юнкцію додаються повністю відповідні констітуенти одиниці.
6. Якщо є можливість, скорочуємо отриману формулу шляхом винесення загальних членів за дужки.
Приклад. Розглянемо функцію чотирьох змінних. Нехай СДНФ заданої функції має вигляд:
Кожну конституенту одиниці наведеної функції відзначаємо одиницею у відповідній клітинці карти Карно (див. Рис. 23). Для наочності прямокутники, що покривають одиниці, відзначаємо овальними лініями. Мінімальна ДНФ даної функції має вигляд:
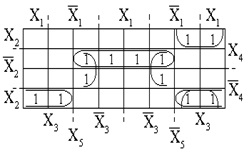
Карта Карно для функції п'яти змінних показана на рис. 24. Для функції шести змінних ¾ на рис. 25. Карти Карно для функцій п'яти і шести змінних мають наступні особливості. Склеювати кон'юнкції відповідають одиниці, розташовані всередині карти симетрично щодо центральних осей симетрії.
Приклад. Нехай функція п'яти змінних представлена одиницями, зазначеними на карті Карно на рис. 24. У результаті покриття отримаємо наступну мінімальну ДНФ:
Мінімізацію функції шести змінних розглянемо на прикладі функції, зазначеної одиницями в карті на рис. 25. У результаті покриття отримаємо:
При виписуванні імпліканти, що виходить в результаті покриття одиниць в карті Карно, можна для контролю користуватися наступними залежностями: l = n-k. m = 2 k. де l - число букв в импликанте, отриманої в результаті покриття, m - число одиниць, покритих даними прямокутником, k - число букв, поглинених в результаті склеювання, n - число незалежних змінних у функції.
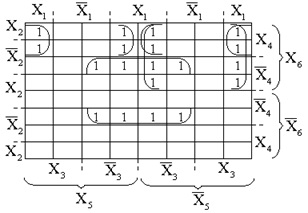
Мал. 25. Карта Карно для функції 6-ти змінних