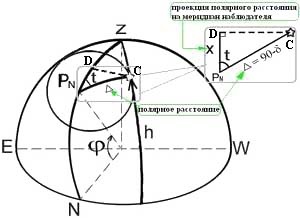
Нехай Полярна зірка знаходиться в довільній точці С. З цієї точки опустимо сферичний перпендекуляр на меридіан спостерігача. Величина х - є проекція полрного відстані на меридіан спостерігача. Так як полярне відстань мало (44 '), то прямокутний трикутник PN CD можна вважати плоским.
З даного прямокутного трикутника маємо x = costм
З малюнка видно, що = ho - x (*)
На підставі основної формули часу, маємо x = сos (S м -).
Підставляючи в формулу (*) значення х, отримуємо = ho - сos (S м -)
Ведемо позначення I = - o сos (S м - o) (**)
o і o - середньорічні значення прямого сходження і полярного відстані Полярної зірки.
Остаточно широта по висоті Полярної зірки визначається наступною формулою
Поправка I враховує добове обертання Полярної зірки навколо північного полюса світу, як видно з формули (**) залежить тільки від зоряного часу і вибирається з ТРАВНІ з таблиці "Широта по висоті Полярної зірки" на сторінках 277-278.
Поправка II враховує сферична трикутника PN CD і коригує поправку I, завжди позитивна, вибирається з ТРАВНІ з таблиці "Широта по висоті Полярної зірки" на сторінці 279 по аргументам S м і h.
Поправка III враховує зміну в перебігу року екваторіальних координат Полярної зірки коригує поправку I вибирається з ТРАВНІ з таблиці "Широта по висоті Полярної зірки" на сторінці 280 по аргументам S м і дата.
І так як всі поправки залежать від зоряного місцевого часу, отже, для визначення широти по висоті Полярної зірки крім виправлення висот необхідно розрахувати зоряне місцевий час, щоб з цього аргументу вибрати поправки I, II і III.
Порядок спостережень і обчислень.