Наближене обчислення коренів рівнянь
Завдання: Відокремити один корінь рівняння і обчислити його на отриманому відрізку [a; b] з точністю до 0,0001 трьома методами.
А) метод дихотомії
Б) метод простої ітерації.
Г) метод хорд.
Рішення:
а) вирішити рівняння методом простої ітерації
Відділимо корінь, для цього перетворимо рівняння до виду:
і побудуємо графіки функцій,.
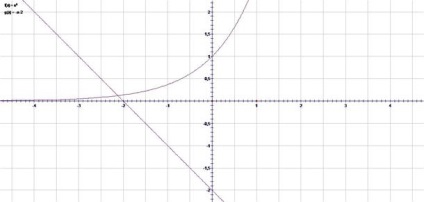
Перетин цих графіків видно на інтервалі [-3; -2], тобто корінь будемо шукати саме на цьому проміжку.
Перетворимо рівняння до виду
.
Виберемо перше наближення.
таким чином з необхідною точністю
б) вирішимо рівняння методом дихотомії (ділення відрізка, на якому відділений корінь, навпіл).
рівняння:
Відрізок, на якому будемо шукати корінь [-3; -2].
на кінцях відрізка функція приймає різні знаки
Розглянемо відрізок [-2,5; -2], тому що на його кінцях функція приймає різні за знаком значення.
Розглянемо відрізок [-2,25; -2], тому що на його кінцях функція приймає різні за знаком значення.
Розглянемо відрізок [-2,125; -2], тому що на його кінцях функція приймає різні за знаком значення.
Розглянемо відрізок [-2,125; -2,0625], тому що на його кінцях функція приймає різні за знаком значення.
Розглянемо відрізок [-2,125; -2,09375], тому що на його кінцях функція приймає різні за знаком значення.
Розглянемо відрізок [-2,125; -2,109375], тому що на його кінцях функція приймає різні за знаком значення.
Розглянемо відрізок [-2,125; -2,1171875], тому що на його кінцях функція приймає різні за знаком значення.
Розглянемо відрізок [-2,12109375; -2,1171875], тому що на його кінцях функція приймає різні за знаком значення.
Розглянемо відрізок [-2,12109375; -2,119140625], тому що на його кінцях функція приймає різні за знаком значення.
Оскільки , То корінь знайдений із заданою точністю
Г) вирішити рівняння методом хорд.
рівняння:
Ітераційна формула має вигляд:
Корінь знайдений із заданою точністю
висновок:
При вирішенні цього рівняння трьома способами отримані коріння:
Значення функції Рівняння: в цих точках відповідно дорівнює
0,00003163
-0,00008037
Тобто Дуже не значимо відрізняється від нуля. Відмінності в значенні коренів в першому, другому і третьому випадку пояснюється різними критеріями зупинки ітераційного процесу