У практичній діяльності ми постійно маємо справу з наближеними величинами, равенствами, формулами: будуємо по точках графіки, витягаємо коріння з чисел, вирішуємо рівняння і т. Д. В теорії наближених обчислень, яка в наші дні швидко розвивається, особливе значення мають методи, придатні для вирішення широкого класу математичних задач. Розповімо про деякі таких методах.
Обчислення довжини окружності за допомогою формул подвоєння - конкретний приклад алгоритму для отримання наближених значень числа π. Цей метод цікавий і з історичної точки зору, так як, можливо, це один з найстаріших прийомів наближених обчислень. Формула подвоєння пов'язує довжини сторін an і a2n правильних n- і 2n-кутників, вписаних в коло (діаметр дорівнює 1):
і дозволяє, почавши з правильного шестикутника, довжина сторони якого дорівнює 1/2, обчислювати послідовно a12. a24. a48. ..., поки не прийдемо до значення периметра, який відповідає заданій точності обчислень. При цьому можна довести, що
π - nan <6/n 2. n ≥ 3.
Це нерівність дозволяє не тільки встановити той факт, що процес сходиться (т. Е. Π - nan → 0 при n → ∞), а й спланувати обчислення заздалегідь. Так, якщо нам потрібно забезпечити точність обчислень, що дорівнює 10 -3. то досить взяти n таким, щоб виконувалася нерівність 6 / n 2 <10 −3. т. е. n> √6000, або n ≥ 78> √6000.
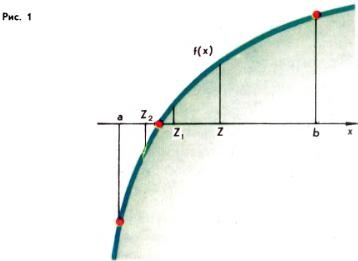
Метод вилки, застосовуваний при знаходженні коренів рівняння f (x) = 0 для безперервних функцій f, носить досить загальний характер. Нехай f визначена і неперервна на відрізку [a, b], має там єдиний корінь і f (a) <0, f(b)> 0. Розглянемо значення f (z), де z = (a + b) / 2 - середина відрізка [a, b]. Якщо f (z) = 0, то z - шуканий корінь. Якщо ж f (z) ≠ 0, то з двох відрізків [a, z] і [z, b] виберемо той, для якого значення функції f на його кінцях мають різні знаки (на рис. 1 це відрізок [a, z] ), і позначимо його через [a1. b1] тим самим f (a1) <0 и f(b1 )> 0. Якщо тепер взяти точку z1 = (a1 + b1) / 2, то знову або f (z1) = 0, або f (z1) ≠ 0. У другому випадку з двох відрізків [a1. z1] і [z1. b1] вибираємо той, на кінцях якого функція f приймає значення різних знаків (на рис. 1, [a2. b2] = [a, z1]). Якщо ми будемо продовжувати цей процес, то він або обірветься на певному етапі, або ми отримаємо послідовність вкладених відрізків [a, b], [a1. b1] [a2. b2], ..., для яких an ≤ an + 1
Крім того, маємо нерівності:
які дозволяють планувати розрахунки із заданою точністю.
Застосування похідної при вивченні поведінки функції дозволяє отримати багато корисних формул для наближеного обчислення значень функцій. З визначення похідною слід, що при малих збільшеннях Δx аргументу x0 для функції f можна написати наближена рівність
Геометрично це означає, що поблизу точки x = x0 ми графік функції y = f (x) замінили графіком дотичної до графіка y = f (x) в точці з абсцисою x = x0 (рис. 2).
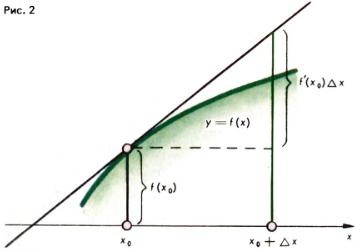
Так, наприклад, виходять наближені формули (ефективні для малих Δх):
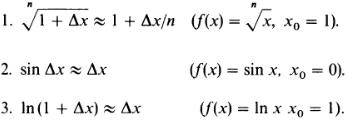
Метод дотичних Ньютона для наближеного рішення рівнянь f (x) = 0 полягає в наступному. Припустимо, що функція f має єдиний корінь c в інтервалі] a, b [і диференційована в кожній точці інтервалу] a, b [і f '≠ 0 в цьому інтервалі. Візьмемо довільну точку x0 ∈] a, b [і напишемо рівняння дотичної до графіка функції f в точці з абсцисою x = x0.
Графіки f (x) і її дотичній близькі між собою при малих x - x0. і тому природно очікувати, що точка x1 перетину графіка дотичній з віссю абсцис буде розташована недалеко від кореня c (рис. 2). маємо:
Продовжуючи цей процес, ми отримаємо послідовність (xn) точок, визначених за допомогою формули
Відомо, що має місце також нерівність
де A> 0 - деяка постійна, яка не залежить від n. Це нерівність показує, що вже при досить малих n виходить досить висока точність наближень.
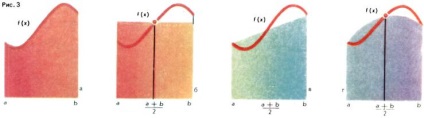
Наближене обчислення площ (інтегралів) криволінійних трапецій (рис. 3, а) засновано на простих геометричних розглядах. Якщо відрізок [a, b], a Якщо замінити графік функції на відрізку [a, b] не прямолінійно відрізком, а графіком параболи (рис. 3, г) і в якості наближення для S взяти площу криволінійної трапеції, обмеженою дугою цієї параболи, то отримаємо формулу Інтегральне числення дає можливість більш точно обчислити площу криволінійної трапеції.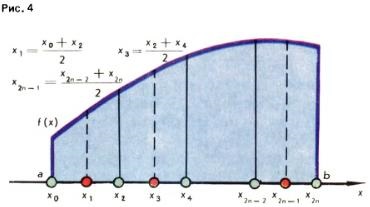
Щоб домогтися можливо меншою помилки при наближених обчисленнях S, проміжок від a до b розбивають попередньо на 2n рівних частин. Тоді дуга графіка y = f (x) розбивається на n частин (рис. 4). Якщо тепер для кожної з цих маленьких дуг використовувати попередні способи наближення, то для площі S вийдуть наближені значення у вигляді сум площ n криволінійних трапецій; маємо:
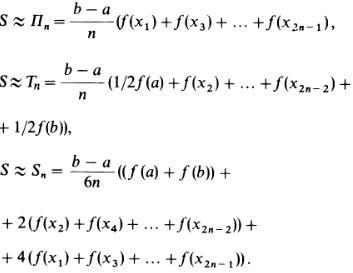
Перші дві формули носять назви формули прямокутників і формули трапецій, а остання - формули Сімпсона, по імені англійського математика Т. Сімпсона (1710-1761).
Оцінки похибки в цих наближених формулах на практиці підраховуються наступним чином. Вибирають число n, кратне 4, і знаходять значення S по формулі Сімпсона (більш точної з цих трьох) з числом точок n і n / 2 (Sn і Sn / 2) і наближено визначають помилку обчислень за допомогою співвідношення