1. Числа точні і наближені
При обробці фізичного експерименту треба розрізняти точні іпрібліжённие числа.
Точними числами є числові коефіцієнти і показники ступеня в формулах; коефіцієнти, що відображають кратність і дольность одиниць виміру; числа, задані визначеннями, і інші. Наприклад, точними є: коефіцієнт 4/3 і показник ступеня 3 у формулі обсягу кулі
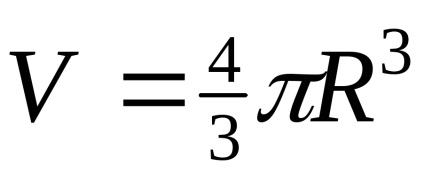
Похибка точних чисел дорівнює нулю.
До наближеним числах відносяться: результати вимірювань различ-них величин; округлені значення точних чисел; табличні значення математичних, фізичних, хімічних величин; ірраціональні чис-ла і інші. Наприклад, наближеними числами будуть: виміряна з по-міццю амперметра сила струму в ланцюзі I = 42,8 мА; прискорення сили тяжіння g = 9,8 м / с 2; постійна Больцмана k = 1,3810 -23 Дж / К; число = 3,14; 2 = 1,41; 1n 10 = 2,30; sin 15 ° = 0,259.
2. Значущі цифри
Значущими цифрами числа називаються всі його цифри, в тому числі і нулі, якщо вони не розташовані на початку числа. Так, числа 3,1416; 5,09410 5; 0,0172 мають відповідно п'ять, чотири і три значущі циф-ри. Можна сказати інакше: перше число - п'ятизначне, друге - чотирьох-значне, третє - тризначне.
Значущою цифра називається тому, що вона є представи-телем того чи іншого розряду або, як кажуть, означає відповідний десятковий розряд. Так, в наближеному числі 4,50 цифра 4 означає розряд одиниць, цифра 5 - розряд десятих часток, цифра 0 - розряд сотих часток. Тисячні і інші більш дрібні частки невідомі, тому соот-ветствующие розряди не відзначений ніякими цифрами.
У точних числах (на відміну від наближених) представники Неозой-чення розрядів відомі - це нулі. Слід застерегти від часто допустимої при обчислення помилки, коли це положення не має рацію-мірно переноситься і на наближені числа. У разі точних чисел чис-ла 4,5 та 4,50 абсолютно рівноцінні, а в разі наближених немає: пер-ше містить дві значущі цифри, друге - три, в першому числі соті частки невідомі, у другому відомі - їх нуль.
Нулі, що стоять на початку числа, не є значущими. Наприклад, в наближеному числі 0,0172 тільки три значущі цифри. Перші два нуля є незначущими, так як відіграють допоміжну роль: слу-жать для вказівки відповідних десяткових розрядів наступними цифрами (цифрами 1, 7 і 2). Така вказівка можна здійснити іншими способами, обходячись без нулів на початку числа, наприклад, записавши його в нормальній формі: 0,0172 = 1,7210 - 2.
В нормальній формі першу значущу цифру наближеного числа ставлять в розряд одиниць, а решта (загальна їх кількість, природно, зберігається) - в десяткових розрядах після коми. Отримане число множиться на множник виду 10 n. де п-ціле позитивне або від-від'ємне число. Наприклад, число 1980 нормальній формі запишеться у вигляді 1,98010 3.
3. Вірні, сумнівні і помилкові цифри
Наближені числа, отримані в обчисленнях, певні з таблиць або знайдені іншими способами, містять різну количес-тво значущих цифр, серед яких є вірні, сумнівні іневерние цифри.
Вірними цифрами наближеного числа називаються п перших цифр, якщо абсолютна похибка числа не перевищує половини оди-ниці розряду n-й цифри. Наприклад, в наближених числах 1406 ± 2; 512,9 ± 1,2; (82,4 ± 0,8) 10 3 вірними відповідно є три, дві і одна перші значущі цифри. Отже, кількість вірних цифр в при-наближенні числі однозначно визначається його абсолютною похибкою-ністю.
Цифра, що стоїть за останньою вірною, є не цілком точно визна-діленої (в ній міститься похибка) і тому називається Зімніть-котельної. У деяких випадках сумнівних цифр може бути дві. У наведеному вище прикладі сумнівними відповідно є од-на, дві і дві останні значущі цифри. Сумнівні цифри прибл-женного числа так само, як і вірні, визначаються його абсолютної по-похибкою.
Всі цифри наближеного числа, що стоять після останньої Зімніть-котельної, є невірними. Дійсно, оскільки ця Зімніть-кові цифра не може бути визначена точно, то цифри наступних нижчих розрядів неможливо знайти і навіть оцінити. Тому невер-ні цифри не містять реальної інформації, безглузді і повинні бути відкинуті (з використанням правил округлення). Наприклад, в при-наближенні числі 406,59 ± 2 п'ять значущих цифр. З них дві перші вер-ні, третя сумнівна, а дві останні невірні. Тому правиль-ної буде запис: 407 ± 2. У разі наближеного числа 210,324 + 1,2 сле-дует писати 210,3 ± 1,2.