Нарисна геометрія по Матвєєвої. Зразки оформлення тут
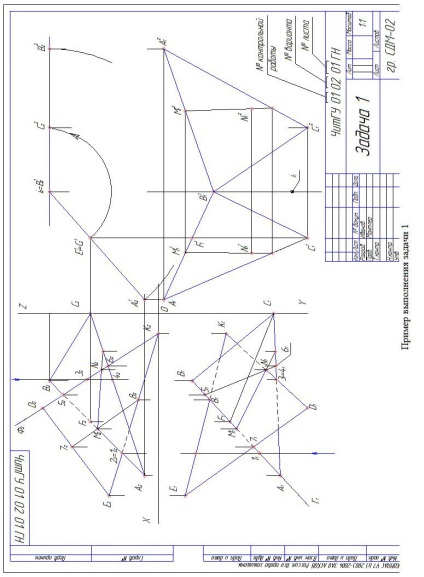
Завдання 1. Побудувати лінію перетину трикутників АВС і EDK і показати видимість їх в проекціях. Визначити натуральну величину трикутника АВС. Дані для свого варіанту взяти з табл. А.1. У лівій половині аркуша намічають осі координат і з табл. А.1. відповідно до свого варіанту беруть координати точок А, В, С, D, E, K вершин трикутників

Обидві площини займають загальне положення, тому застосовуємо метод січних площин. Для побудови лінії перетину площин будують точки перетину двох прямих одній площині з іншого і через них проводять шукану лінію. 1. Пряму DK укладають в допоміжну площину Ф2 ┴ П2. 2. Знаходять лінію перетину площин Ф2 ∩ Δ АВС = 52 62
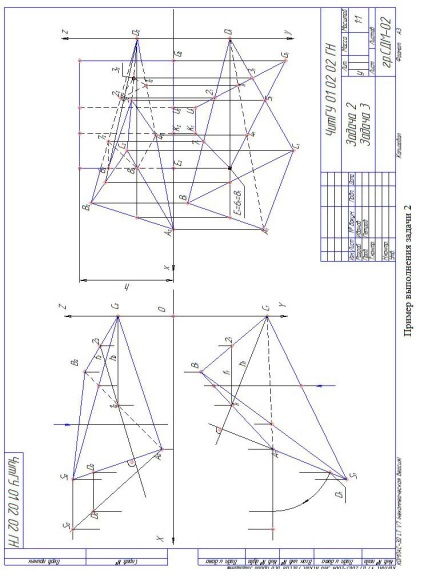
Завдання 2. Побудувати проекції піраміди, підставою якої є трикутник АВС, а ребром SA визначають висоту h піраміди. Дані для свого варіанту взяти з табл. А.2. У лівій половині аркуша намічають осі координат і за координатами будують проекції підстави. Через точку А до площини трикутника проводиться перпендикуляр
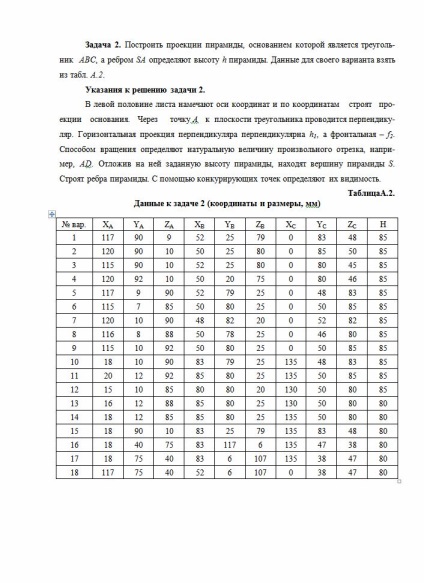
Горизонтальна проекція перпендикуляра перпендикулярна h1. а фронтальна - f2. Способом обертання визначають натуральну величину довільного відрізка, наприклад, АD. Відклавши на ній задану висоту піраміди, знаходять вершину піраміди S. Будують ребра піраміди. За допомогою конкуруючих точок визначають їх видимість
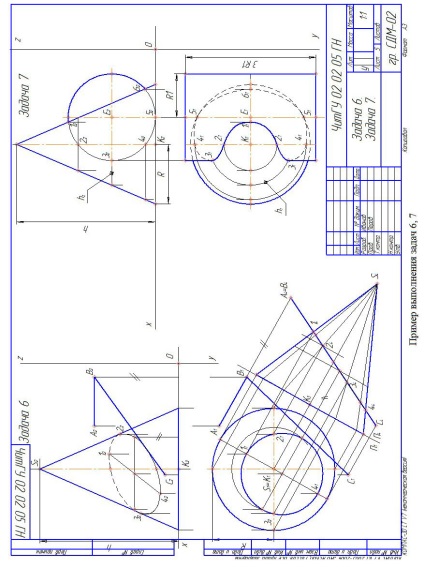
Завдання 6. Побудувати лінію перетину конуса обертання площиною АВС загального положення. У лівій половині аркуша будують проекції конуса обертання і площини АВС. Конус і площину займають загальне положення. Завдання вирішуємо способом заміни площин проекції. Горизонтальну і фронтальну проекції еліпса перетину будують за належністю

Завдання 7. Побудувати лінію перетину конуса обертання з циліндром обертання. Осі поверхонь обертання - взаємно перпендикулярні проектують перехресні прямі. Дані для свого варіанту взяти з табл. А.6. У правій половині аркуша будують проекції конуса обертання і циліндра обертання
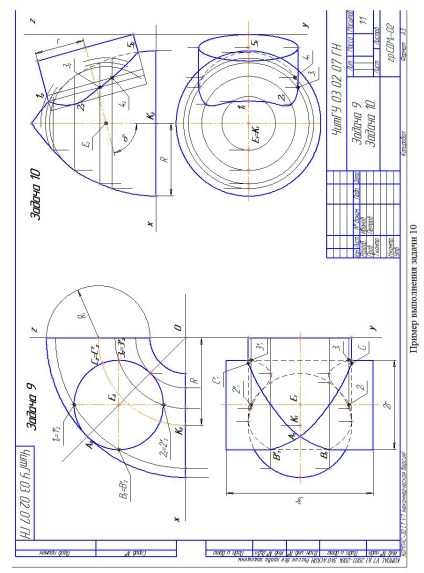
Завдання 10. Побудувати лінію перетину закритого тора з поверхнею похилого циліндра обертання. Поверхні мають загальну фронтальну площину симетрії. За заданими координатами будують проекції похилого циліндра обертання і закритого тора. Радіус циліндра обертання визначають за формулою r = 2R / 3

Головним меридіаном поверхні тора є дуги кіл радіуса 2R, центр кіл лежать на екваторіальній паралелі. Обидві поверхні займають загальне положення. Застосовуємо метод січних сфер, так як тут виконані три умови: 1) обидві поверхні обертання; 2) осі поверхонь перетинаються; 3) осі поверхонь лежать в площині, паралельній П2

Завдання 10. З точки перетину осей як з центру проводиться сфера довільного радіуса. Вона перетинає обидві поверхні по колах. Фронтальна проекція кіл зображується відрізками прямих ліній, які перетинаються в точках, які є фронтальними проекціями шуканої лінії перетину поверхонь