Музичним ладом називається система інтервальних відносин рядузвуків, розташованих в порядку послідовності їх частотного підвищення або зниження.
Основою таких математичних ладів, що зробили помітний вплив на весь хід розвитку європейської музичної культури, вважають лад, створений давньогрецькими вченими і назвати Піфагорійський (по імені відомого математика Піфагора). При виборі звуків для музичного використання основну роль зіграло відносне благозвучаніе інтервалів октави, квінти і кварти.
Давньогрецьким вченим Орфею і Піфагору вдалося на монохорде показати, що нові звуки можна отримати не тільки шляхом
збудження цілої струни, але і її частин (1/2 струни, 2/3 і 3/4), і що ці звуки утворюють з її основним тоном інтервали октави (1/2 струни), квінти (2/3 струни) і кварти (3/4 струни).
Ці інтервали вперше були застосовані для настройки ліри Орфея, яка мала 4 струни, порушувані дерев'яним ударнічком.
Знання зазначених інтервалів і їх інтервальних коефіцієнтів (1/2, 2/3 і 3/4) дозволило утворити різні звукоряди.
З найпростіших звукорядов можна назвати трехступенную гаму Орфея, пятіступенную китайсько-шотландську гаму і семіступенную Піфагорійський гаму.
Звукоряд гами Орфея: (с інтервальним коефіцієнтом 3/4 і 1/2)
Звукоряд китайсько-шотландської гами має п'ять звуків, утворених від основної ноти до вгору і вниз квінтового ходами по два рази:
Отримані звукісведени потім в одну октаву:
Звукоряд Піфагорійський гами утворений п'ятьма ходами від ноти до по квинтам вгору і одним квінтовим ходом вниз:
Розташувавши отримані звуки квінтового ходами в порядку їх висоти в малу октаву і підписавши під ними відповідні частини струни (коефіцієнти), отримаємо диатоническую мажорну гаму Піфагорійський ладу:
Однак Піфагорійський лад не отримав широкого поширення, так як він не має енгармонічно рівних звуків, в зв'язку з чим настройка музичних інструментів з фіксованим звукорядом (орган, клавесин, рояль) виявилася досить складною операцією, практично нездійсненним.
Математичні розрахунки показали, що Піфагорійський лад є незамкнутим на величину 1/9 тону, яка називається
Піфагорійський Ком, що вносить розлад у логічне математична побудова натурального ладу.
Рівномірна темперації призводить звуки в послідовну злагодженість звукового діапазону, що дозволяє вільно модулювати при грі на музичному інструменті з фіксованим звуками.
Математична сутність рівномірної темперації в межах однієї октави полягає в наступному. Відомо, що число коливань верхнього звуку будь октави в два рази більше числа коливань її нижнього звуку, значить, октавний коефіцієнт дорівнює двом. Але кожна темперована октава складається з 12 рівних (за ступенями) півтонів. Звідси можна зробити розрахунок інтервального коефіцієнта, на величину якого відрізняється частота кожного наступного півтони від попереднього. Для цього треба знайти так званий множник темперации:
Знаючи інтервальний коефіцієнт темперованого півтони і число півтонів, що входять в хроматичну двенадцатізвуковую гаму, а також в діапазон звуків, наприклад фортепіано, і вважаючи, що ЛЯ першої октави відповідає 440 Гц, можна знайти число коливань для всіх звуків темперованого хроматичної гами і для всього діапазону. Отримані таким чином числа коливань півтонів наведені в табл. 1.
Однак число коливань звуків, що входять до складу діапазону фортепіано (або іншого інструменту), є тільки основою, яка вказує, з якою частотою повинен коливатися звукообразователь (струна), але воно не розкриває характеру звучання настроюються інтервалів звукорядов. Характер, а також узгоджене або неузгоджене звучання розкривають і визначають уважним прослуховуванням настроюються окремих звуків, інтервалів і акордів, а також виділяючи при цьому число биття в секунду.
Відомо, що при гармонійному відтворенні чистої квінти її третій частковий тон (обертон) нижнього звуку утворює тон збіги з другим частковим тоном її верхнього звуку. У темперированной квінті зазначені часткові тони не збігаються, і між ними виникають биття. Для квінти число биття в секунду одно 0,89 (табл. 1), так як число коливань третього часткового тону звукасоставляет 784,89, а число коливань другого часткового тону звуку-784.
Число биття в секунду для квінти одно 1,05, так як число коливань третього часткового тону звуку
становить 933,38, а число коливань другого часткового тону звукасоставляет 932,33. За цих же міркувань число
биття в секунду для квінтиравно 1,25, а для квінтиравно 1,41.
З цього видно, що для настройки темперованого квінт необхідно знайти число биття для всіх 12 квінт. Однак практика настройки музичних інструментів з фіксованою частотою звуків показує, що ці тонкощі при формуванні ладу є орієнтиром для теоретичного обґрунтування темперации. Практично ж для всіх 12 квінт можна взяти середнє число биття, т. Е. Для квінт першої октави 1,1, так як:
Ця заміна значно спрощує процес налаштування темперованого квінт і дає мізерно мале розходження між ви чисельними інтервалами 12-звукового рівномірно темперованого ладу і налаштованими квінтового інтервалами з утворенням 1,1 биття в секунду.
Основним завданням налагоджувальника є уловлювання на слух і підрахунок цих биття при встановленні темперации.
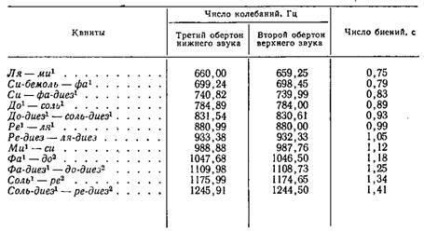
Вище наведена таблиця чисел коливань третього і другого обертонів і частоти биття між ними для квінтових інтервалів-лов рівномірно темперованого ладу. З таблиці видно, що в міру підвищення звуків збільшується не тільки число коливань третьої і другої гармонік, але і частота їх биття.
Наведені в таблиці квінти відносяться до середньої частини звукового діапазону фортепіано, де квінтові співзвуччя і їх биття найкращим чином прослуховуються при налаштуванні. На цій ділянці звукового діапазону настройка квінт може бути проведена з достатньою точністю, в середньому до одного биття в секунду.
До того ж під час налаштування цілі числа биття легше відраховувати, що також сприяє більш швидкому і правильному темперування звуків, що входять в зону темперации (ділянки звукового діапазону середнього регістра, що настроюється в темперований квінтові або квартовий інтервали, називається зоною темперации).
Отже, якщо під час налаштування дванадцяти квінт, що входять в зону темперации, ми налаштували їх так, що кожна квінта виявиться звуженої (зменшеною по інтервалу) до одного биття в секунду (в порівнянні з чистим квінтою), то ми з достатньою точністю налаштуємо кожну з них як темперований. При цьому останній звук збігається з першим, з якого почали настройку, і заключна квінта також буде звучати з одним биттям в секунду і також буде звуженою на ту ж величину. При дотриманні зазначеного порядку квінтовий коло вийде замкнене, все півтонни - рівними, а все однойменні інтервали і співзвуччя в будь-яких тональностях будуть однорідними за характером звучання і ступеня консонансних і дисонансні.
Темперації звуків, що входять в цю ж ділянку діапазону, можна отримати і при налаштуванні по квартовим ходам (або по квартовий колі). Однак, з огляду на, що биття у них з'являється між четвертою гармонікою нижнього звуку і третьої верхнього, частота биття буде більше, ніж в темперований Квінта.
Налаштування фортепіано. Функціональність биття.
Пам'ятка для музиканта і налагоджувальника фортепіано
Биття виникають на тлі неповного збіги як основних, так і часткових тонів (обертонів), що входять в резонанс один з одним. Наприклад, в інтервалі велика терція від звуку ЛЯ малої октави (основний тон 220 Гц) до звуку ДО-дієз (основний тон 277,1 Гц) 5-ий обертон нижнього звуку входить в резонанс з 4-х обертоном верхнього звуку (1100-1108 , 5 Гц). На тлі резонансу виразно чутні 8,5 биття в секунду. Биття можна порівняти з ударами молоточка по струнах, тільки на значно більш тонкому слуховому рівні. Діапазон чутності обертонових биття для людини знаходиться в межах від 0 до 30 биття в секунду. Найгучніші і грубі биття виникають між основними тонами і їх найближчими обертонами (2-й і 3-й). Діапазон їх чутності доходить до 60 биття в секунду. Більш докладно про биття можна прочитати в книзі «Музична акустика» Н.А. Гарбузова, що вийшла в 1954 році. Людина не встигає прослуховувати обертонового биття в процесі звучання музичного тексту, але вони реально звучать і впливають на нього підсвідомо. При повільному прослуховуванні інтервалів на фортепіано після невеликого тренування слуху биття дуже добре прослуховуються і підраховуються (до 30 биття в секунду).
Характеристика обертонових биття у всіх 13 основних інтервалах *
Все биття в інтервалах даної таблиці наведені від звуку ЛЯ малої октави (220 Гц). Кількість биття в кожному наступному інтервалі (по хроматичним півтонів) поступово збільшується, і пройшовши повну октаву, відбудеться подвійне кількісне збільшення числа биття.
Ознайомившись з обертоновой характеристикою інтервалів (див. Таблицю 1), вибір методу настройки фортепіано може бути найрізноманітнішим залежно від здібностей в прослуховуванні биття конкретною людиною.
- Найлегший спосіб настройки (грубе налаштування) може бути виконаний майже будь-яким музикантом. Необхідно по камертону налаштувати звук ЛЯ 1-ої октави (440 Гц), від нього вниз звук ЛЯ малої октави (220 Гц). Тепер в межах отриманої октави (зона темперации) будь-якими ходами вгору-вниз чистими квінтами, звуженими на 1 биття в секунду (усереднене число биття для всіх Квінт) і чистими квартами, розширеними на 1,5 биття (усереднене число биття для всіх кварт), налаштовуємо все хроматичні звуки зони темперации. Далі октавними ходами налаштовуємо весь діапазон звуків фортепіано.
- Значно кращий результат дає настройка по великим, терціях (розширеними від чистої терції на 8,5-14 биття) і великим секстою (розширеними на 10-13 биття). Необхідно пам'ятати, що кількість обертонових биття, в будь-яких інтервалах, поступово пройшовши октаву вгору, збільшується рівно в два рази.
- Налаштування найвищої якості (з точністю до 1/200 частки від тону) виконується по малим терціях, звуженим на 12-23 биття і звуженим на 14-23 биття малим секстою. Таку настройку може виконати тільки настроювач вищої кваліфікації з унікальним слухом, знанням теорії музичного ладу і великим досвідом роботи.
Обертонового биття дуже швидко розбудовуються і тому фортепіано необхідно налаштовувати через кожні 2-3 місяці. У філармонійних і концертних залах фортепіано налаштовується перед кожним концертом. Перевірка налаштованого інструменту проводиться по складовим інтервалах, квінтдецімамі, а також великими і малими децима, що мають обертонового характеристики великих і малих терцій.
Про функціональність обертонових биття
З усього вищесказаного можна зробити вкрай важливий висновок. Напруженість в інтервалах повністю залежить від загальної кількості чутних в них биття. З таблиці 1 видно, що обертонового биття вишикувалися в чітку кількісну функціональну систему. Наш слуховий досвід в напруженості інтервалів повністю підтверджений чіткої функціональністю биття. Музикантам, теоретикам музики і особливо композиторам необхідно пам'ятати, що функціональність биття в інтервалах - головна виразна функція в гармонії, так як з інтервалів складаються всі акорди і будь-які поєднання гармонійних звуків. Цілком ймовірно, все розвиток музики на протязі тисячоліть йшло в пошуках і в усвідомленні функціональності обертонових биття як найтоншої і в той же час найпотужнішою виразною функції гармонії.