Постановка завдання оптимізації «Дана якась функціяf (x1, x2, ..., xn), яку прийнято називати цільової. Необхідно знайти або максимум, або мінімум цієї функції за умови виконання деяких додаткових обмежень. Завдання пошуку max і min легко перетворюються один до одного (множенням цільової функції на -1). Додаткові обмеження вводяться в загальному вигляді як якісь нелінійні нерівності:
обмеження можуть представлятися у вигляді нерівностей, і у вигляді рівності.
Загальна задача оптимізації.
По виду цільової функції і обмеження завдання оптимізації прийнято ділити на наступні види.
Якщо цільова функція лінійна і обмеження теж лінійні, то таке завдання називається завданням лінійного програмування. Завдання ЛП вивчені добре, тому існує метод лінеаризації - перетворення завдань нелінійних до лінійного вигляду.
Якщо цільова функція представляється квадратичною формою, то завдання називається задачейквадратічного програмування. Нелінійні задачі теж часто призводять до квадратичної, оскільки вирішити квадратичную завдання часто легше, ніж задачу загального вигляду.
В даний час продовжує розвиватися теорія кубічного програмування. Вона ще до кінця не розроблена.
Якщо обмеження на цільову функцію відсутня або мають простий вигляд xia (обмеження тільки на змінну), то таке завдання називається завданням безумовної оптимізації.
Якщо функція нелінійна і існує обмеження (складні), то задача відноситься до нелінійної оптимізації.
Якщо в задачі існують параметри, що залежать від часу, при цьому вони істотно впливають на рішення, то в кожен момент часу (загальний час розбивається на кілька етапів) оптимальне рішення виходить різний і підсумкове оптимальне рішення вдає із себе суму рішень прийнятих на кожному етапі. Методи вирішення таких багатоетапних завдань відносяться до методів теорії динамічного програмування.
У задачі лінійного програмування (лп) цільова функція може бути представлена як сума добутків змінних на якісь константи:
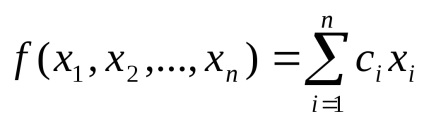
Обмеження завдання можуть бути представлені у вигляді рівностей і нерівностей:

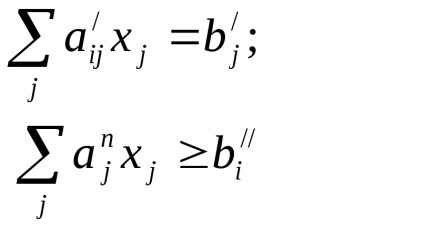
(Обмеження у вигляді рівності) (обмеження у вигляді нерівностей)
Сукупність хi називається вектором невідомих. Рішенням завдання тоді буде значення цього вектора невідомих, при якому функція f має максимумом або мінімумом. Коефіцієнти ci також утворює вектор, який називається вектором ресурсів. Елементи bi утворюють вектор з назвою вектор запасів. Для зручності рішення прийнято приводити задачу від загальної постановки до спеціального стандартного вигляду.
Вимоги до стандартного вигляду завдання лп:
Параметри хi повинні бути більше або дорівнювати нулю (хi 0). Якщо є таке обмеження, яке допускає від'ємне значення хi. то роблять заміну змінних так, щоб нове хi не було негативним.
Обмеження у вигляді нерівностей перетворюються в обмеження у вигляді рівності.
Елементи, які стоять праворуч повинні бути невід'ємними в равенствах, тобто bi 0.