Нормальне рівняння площини

Три крапки в просторі. і. що не лежать на одній прямій, визначають єдину площину. Очевидно, що точка лежить в цій площині тоді і тільки тоді, коли вектори

компланарність. Відповідно до критерію компланарності це рівнозначно тому, що мішаний добуток зазначених векторів дорівнює нулю:

Остання рівність і є рівнянням площини, що проходить через дані три точки. Якщо розписати цей визначник (наприклад, за елементами першого рядка), то отримаємо загальне рівняння площини.

Нехай площину визначається завданням вектора нормалі. опущеного на площину з початку координат і довжиною цього вектора. Нехай також. . - кути, утворені вектором з координатними осями. і. Тоді одиничний, сонаправленнимі з вектором. вектор має координати:. Точка лежить в зазначеній площині тоді і тільки тоді, коли справедливо рівність

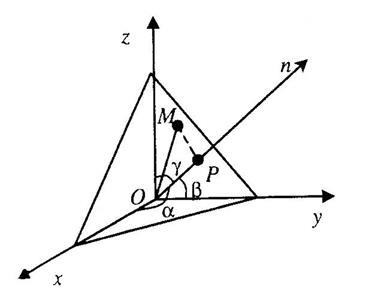
то критерій приналежності точки розглянутій площині може бути описаний рівністю:

Отримане рівність є рівнянням даної площини, званим її нормальним рівнянням.

Відхиленням точки від даної площини називається відстань від цієї точки до площини, взяте зі знаком плюс, якщо точка і початок координат лежать по різні боки від даної площини, і взяте зі знаком мінус, якщо точка і початок координат лежать по одну сторону від даної площини.

Розглянемо довільну точку простору. Спроектуємо цю точку на вектор. Нехай - отримана проекція. Відхилення точки від даної площини одно. Очевидно, що

Іншими словами, для знаходження відхилення точки від площини слід в ліву частину нормального рівняння площини підставити замість. і координати цієї точки. Очевидно, що відстань від точки до площини визначається рівністю:

Відзначимо, що загальне рівняння площини

Можна привести до нормального вигляду так, як це робилося для рівняння прямої на площині. Для цього потрібно підібрати число таке, що

Зводячи в квадрат перші три рівності, складаючи їх і з огляду на, що сума квадратів напрямних косинусів дорівнює одиниці, отримаємо:

З рівності випливає, що знак повинен вибиратися протилежним знаку вільного коефіцієнта. Число. визначається таким чином, називається нормує множником. Якщо помножити обидві частини загального рівняння на нормуючий множник, то будемо мати нормальну рівняння. Відповідно до цих міркуваннями робимо висновок, що відстань від точки до площини визначається формулою:

Приклад. Знайти нормальне рівняння площині, що проходить через точки. . .

# 8710; Скористаємося формулою для знаходження рівняння площини, що проходить через задані три точки. і:

В результаті отримаємо:

Отримане рівняння є загальним рівнянням площини. Наведемо його до нормального вигляду. Для цього знайдемо нормирующий множник:

Помножимо обидві частини загального рівняння площини на знайдений нормирующий множник:

Це і є нормальне рівняння даної площини. ▲