Знаходження моменту інерції - обчислювальна задача. Знайдемо моменти інерції для найпростіших геометрично правильних форм твердого тіла, маса якого рівномірно розподілена за обсягом.
Момент інерції обруча щодо осі перпендикулярно його площині і проходить через його центр.
Обруч будемо вважати нескінченно тонким, т. Е. Товщиною обода можна знехтувати в порівнянні з радіусом R. Оскільки в цій системі все маси знаходяться на однаковій відстані від осі обертання, R 2 можна винести з-під знака інтеграла:
де - повна маса обруча.
Момент інерції диска відносно осі, перпендикулярної його площині і проходить через центр.
Диск будемо вважати нескінченно тонким, т. Е. Його товщина значно менше радіуса R. Момент інерції, згідно з визначенням, величина адитивна: момент інерції цілого тіла дорівнює сумі моментів інерції його частин. Розіб'ємо диск на нескінченно тонкі кільця радіусом г і шириною dr.
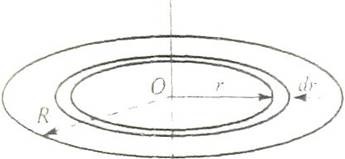
Площа виділеної кільця дорівнює добутку його довжини ок-ружності на ширину кільця: 2πrdr. Оскільки маса m диска розподілена рівномірно, то маса одиниці площі диска дорівнює m / (πR 2).
dm = 2πrdr (m / πR 2) = (2m / πR 2) rdr.
Момент інерції кільця:
dI = drm 2 = (2m / πR 2) r 3 dr.
Підсумуємо моменти інерції всіх таких кілець:
.
Момент інерції кулі відносно його діаметра.
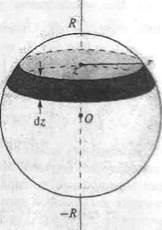
Розіб'ємо кулю на нескінченно тонкі диски товщиною dz. що знаходяться на відстані z від центру кулі. Радіус такого диска:.
Обсяг диска dVz дорівнює його площі, помноженої на товщину:
dVz = πr 2 dz. Масу виділеного диска dm знаходимо, розділивши масу кулі т на його обсяг 4πR 3/3 і помноживши на обсяг диска:
.
Момент інерції диска в даному випадку:
.
Момент інерції кулі знаходиться інтегрування з усіх вищевказаних дисків:
.
Момент інерції тонкого стержня відносно осі обертання, що проходить через його середину перпендикулярно стрижню.
Нехай стрижень має довжину l. Направимо вісь х вздовж стрижня. Початок координат нехай перебуває на середині стрижня. Візьмемо елемент стержня довжиною dx. що знаходиться на відстані х від осі обертання. Його маса дорівнює dm = (m / l) dx. а момент інерції стрижня - dI = dmx 2 = (m / l) x 2 dx
Звідси знаходимо момент інерції стержня:
Для визначення моменту інерції тіл з обертальної симетрією використовується маятник Максвелла. У ньому досліджуване тіло здійснює складний плоско-паралельний рух. Невеликий диск (маховичок), насаджений туго на вісь, опускається під дією сили тяжіння на двох нитках, попередньо намотаних на вісь маховичка. Нитки під час руху розмотуються до повної довжини, розкрутити маховичок продовжує обертальний рух в тому ж напрямку і намотує нитки на вісь, внаслідок чого він піднімається вгору, сповільнюючи при цьому обертання. Дійшовши до верхньої точки, диск знову опускається вниз і т. Д. Маховичок буде вдосконалення-шать коливання вгору і вниз, тому пристрій називають маятником.
Рух маятника Максвелла можна розглядати як складне, що складається з поступального руху вниз і обертального навколо своєї осі симетрії. Поступальний рух описується відповідним рівнянням динаміки, яке ми запишемо в проекціях на вертикальну вісь, що збігається за напрямком з вектором g, де g - прискорення вільного падіння:
Рівняння динаміки для обертальної складової цього руху має такий вигляд в проекціях на горизонтальну вісь, яка відповідає за направленням з вектором М:
де m - маса маятника, 2T - сумарне натяг ниток підвісу, I - момент інерції маятника відносно горизонтальної осі, # 949; - кутове прискорення, М - момент натягу ниток, рівний 2TR. де R - радіус осі підвісу маятника.
Взаємозв'язок між поступальним і обертальним рухами:
де h - шлях, прохідний маятником від верхньої точки до нижньої, t - час руху маятника при проходженні шляху h.
З написаних вище рівнянь отримуємо наступне:
I = mR 2 * (gt 2 / 2h - 1) = md 2/4 * (gt 2 / 2h - 1)
Ця формула виражає момент інерції маятника Максвелла, який складається з осі, диска і кільця.
Таким чином, момент інерції маятника Максвелла можна записати у вигляді:
де I - момент інерції маятника Максвелла, Iо- момент інерції осі підвісу, Iд- момент інерції диска, Ік - момент інерції накладного кільця.
Аналогічно можна записати і масу маятника Максвелла:
де m - маса маятника Максвелла, mо- маса осі підвісу, mд- маса диска, mк - маса знімного кільця.
Висловимо момент інерції кільця:
Для виключення невідомих величин проведемо експеримент з кільцями різної маси. Запишемо для кожного кільця вираз
Так як зовнішні і внутрішні радіуси кілець однакові, то:
.
Вирішивши систему рівнянь, отримаємо:
,
.
Для третього кільця момент інерції буде дорівнює:
.
Таблиця 1Формули розрахунку моменту інерції
де кг / м 3 - щільність матеріалу, з якого виготовлена вісь і диск; кг / м 3 - щільність матеріалу кільця; Ro - радіус осі; Rд - радіус диска; Rвнеш і Rвн - зовнішній і внутрішній радіуси кільця; # 955; - довжина осі; bд - товщина диска; bк - товщина накладного кільця.
Для визначення моменту інерції тіл обертання будемо використовувати спеціальну установку - маятник Максвелла.
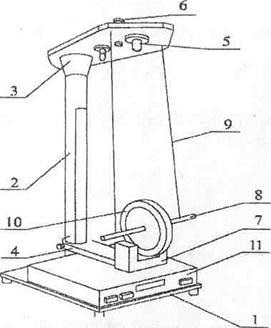
1 - підстава, 2 - стійка, 3 - нерухомий верхній кронштейн, 4 - рухливий кронштейн, 5 - електромагніт, 6 - комірець з фіксатором, 7 - фотодатчик, 8 - вісь із закріпленим на ній диском, 9 - біфілярного підвіс, 10 - змінне металеве кільце, 11 - секундомір.
Вправа 1. Визначення моменту інерції маятника Максвелла.
1. Включаємо в мережу шнур живлення секундомір і натискаємо на кнопку «мережу», розташовану на лицьовій панелі секундоміра. При цьому загоряються лампочки фотодатчика і цифрові індикатори секундомір.
2. Встановлюємо на диску маятника кільце з масою mк1.
3. За шкалою на стійці 2 визначаємо хід маятника h від верхньої точки до нижньої.
h = 23,2 см = 0,232 м
4. Обертаючи маятник, зафіксуємо його в верхньому положенні за допомогою електромагніту, стежачи за тим, щоб нитка намотувалася на вісь виток до витка. Натискаємо на кнопку «скидання» і переконуємося, що індикатор секундоміра обнулився.
5. Плавно натискаємо кнопку «пуск» на мілісекундомере і вимірюємо час ходу маятника t. Вимірювання повторюємо 10 раз. Знаходимо середнє значення ходу маятника tср.
6. Проробляємо пп. 2-5 з кільцями масою mк2 і mк3.
7. Вимірюємо штангенциркулем радіус осі Ro. радіус диска Rд. зовнішній Rвнеш і внутрішній Rвн радіуси трьох кілець з різною масою. Вимірюємо довжину осі # 955 ;, товщину диска bд і товщину накладних кілець bк. Маса диска з віссю дорівнює 120г. Вимірювання виконані з урахуванням поправки на 9,9 мм.
8. Результати всіх вимірювань оформляємо у вигляді таблиці.
Вправа 2. Визначення моменту інерції накладних кілець.
1. Включаємо в мережу шнур живлення секундомір і натискаємо на кнопку «мережу», розташовану на лицьовій панелі секундоміра. При цьому загоряються лампочки фотодатчика і цифрові індикатори секундомір.
2. Встановлюємо на диску маятника кільце з масою mк1.
3. За шкалою на стійці 2 визначаємо хід маятника h від верхньої точки до нижньої.
h = 23,2 см = 0,232 м
4. Обертаючи маятник, зафіксуємо його в верхньому положенні за допомогою електромагніту, стежачи за тим, щоб нитка намотувалася на вісь виток до витка. Натискаємо на кнопку «скидання» і переконуємося, що індикатор секундоміра обнулився.
5. Плавно натискаємо кнопку «пуск» на мілісекундомере і вимірюємо час ходу маятника t. Вимірювання повторюємо 10 раз. Знаходимо середнє значення ходу маятника tср.
6. Проробляємо пп. 2-5 з кільцями масою mк2 і mк3.
7. Вимірюємо штангенциркулем радіус осі Ro. радіус диска Rд. зовнішній Rвнеш і внутрішній Rвн радіуси трьох кілець з різною масою. Вимірювання виконані з урахуванням поправки на 9,9 мм.
8. Результати всіх вимірювань оформляємо у вигляді таблиці.