Розглянемо, як змінюється положення проекцій точки при обертанні її навколо осі, перпендикулярної до площини П1 (рис. 10.10).
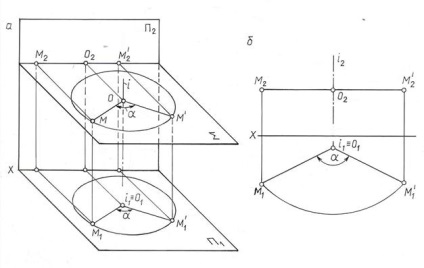
При обертанні точки М навколо осі i ^ П1 (центр обертання О, радіус обертання ОМ ^ i) на кут a. її горизонтальна проекція М1 переміщається по окружності (з центром в точці О1 @ i1) того ж радіуса, в ту ж сторону і на той же кут a. що і сама точка М. Траєкторія руху точки М в просторі на площину П1 проектується без спотворення, тому що вона належить площині # 931 ;. паралельної П1. Фронтальна проекція точки М (М2) переміщається по прямій, паралельної осі ОХ.
Обертання геометричних фігур зводиться до обертання кінцевого числа точок, що визначають цю форму. При цьому корисно мати на увазі наступне:
а) точки, що лежать на осі обертання, не змінюють свого положення, інші точки обертаються в площинах, перпендикулярних осі обертання;
б) всі обертові точки повертаються в одну сторону на один і той же кут;
в) якщо вісь перпендикулярна деякої площини проекцій, то проекції на цю площину обертається фігури в будь-якому її положенні конгруентний. Останнє випливає з розглянутих властивостей методу плоскопараллельного переміщення, тому що обертання навколо осей, перпендикулярних до площин проекцій є окремим випадком цього методу.
Розглянемо, як здійснюється на епюрі переміщення відрізка загального положення в приватне становище шляхом обертання навколо осі перпендикулярної площинам проекцій.
Приклад 1. Відрізок АВ загального положення перетворити в положення паралельне площині проекцій П2.
Щоб здійснити таке перетворення, досить повернути відрізок АВ навколо осі i ^ П1 на кут a. Для скорочення кількості геометричних побудов вісь i # 8715; В (рис. 10.11).
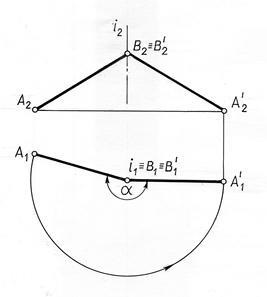
Величина кута a приймається такий, щоб після повороту горизонтальна проекція відрізка зайняла становище || ОХ. Так як точка В належить осі обертання, то вона не буде змінювати свого положення в процесі перетворення, отже, В1 º В1 // і В2 º В2 //. Для знаходження точки А2 / необхідно з А1 // провести вертикальну лінію зв'язку і відзначити точку перетину її в горизонтальній прямій, проведеної через А2.
Обертання навколо ліній рівня застосовують в тих випадках, коли дану плоску фігуру потрібно поєднати з будь-якої площиною, паралельній площині проекцій. У такому положенні плоска фігура проектується на відповідну площину проекцій без спотворення.
На рис. 10.12 показано обертання деякої точки А навколо горизонтальній осі h || П1. В цьому випадку площиною обертання точки А (площину, в якій розташована траєкторія руху точки А - окружність) буде площину # 931 ;. перпендикулярна осі обертання (# 931; ^ h) і, отже, горизонтальній площині проекцій # 931; ^ П1.
Точка А буде переміщатися по колу з центром в точці С (точка перетину осі обертання з площиною # 931; ). С = h ∩ # 931 ;. Радіус цього кола дорівнює відстані від точки А до осі обертання h (R = АС).
площина # 931; - горизонтально проектує (# 931; ^ П1), тому траєкторія руху точки А в просторі (окружність) спроецируется на площину П1 в пряму, збігається з горизонтальним слідом площини # 931; (# 931; П1).
Коли точка А, обертаючись навколо осі h. суміститься з площиною, паралельній площині проекцій П1. радіус обертання цієї точки R = CA займе горизонтальне положення і спроецируется на П1 без спотворення: C1 A1 = CA = R.
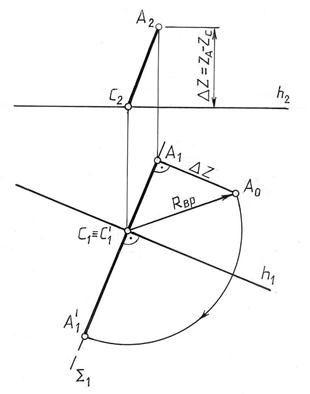
План виконання завдання наступного:
1. Через горизонтальну проекцію А1 точки А проведемо горизонтальний слід площини # 931; (# 931; 1 ^ h1) і відзначаємо центр обертання С (С1 С2).
2. Визначаємо натуральну величину радіуса обертання Rвр. = А0 С1 (як гіпотенузу прямокутного трикутника, катетами якого є горизонтальна проекція радіуса обертання А1 С1 і різниця координат Z точок А і С. # 8710; Z = Zа -ZC). гіпотенуза трикутника # 8710; С1 А1 А0. С1 А0 = Rвр. .
Нове, після повороту, положення точки А1 / знаходиться в місці перетину дуги окружності, проведеної з горизонтальної проекції центру обертання С1 радіусом, рівним С1 А0 з горизонтальним слідом # 931; 1 площині # 931 ;.
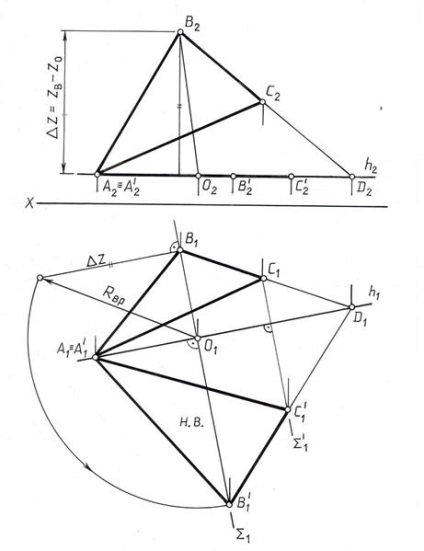
На рис. 10.13 показаний приклад обертання трикутника АВС навколо його горизонталі АD (AD ÌABC. AD || П1). Точки D і А не змінюють свого положення в процесі обертання трикутника (А1 ºА1 /. D1 ºD1 /), тому що вони належать осі обертання h (D Îh. А Îh), а горизонтальні проекції точок В і С переміщаються по прямим, перпендикулярним h1 (B1 B1 / ^ h1 і С1 С1 / ^ h1). Положення точки В1 / після повороту трикутника визначено описаним вище способом (О1 В1 / = О1 В0 = Rвр.). В результаті обертання трикутник АВС зайняв положення А1 / B1 / C1 /, паралельне площині П1. і спроектувати на цю площину без спотворень: çА1 / В1 / C1 / ç= çABC ç. Фронтальна проекція трикутника після повороту А2 / B2 / C2 / - пряма лінія, паралельна осі координат.
Площині, дотичні до поверхонь
Загальні поняття. Способи побудови дотичних площин.
Основні типи завдань з побудови дотичних.
Площиною, дотичною до криволінійної поверхні у звичайній точці А, називається площина, яка визначається двома пересічними прямими, дотичними до цієї поверхні в точці А (рис. 11.1).
Звичайними точками поверхні є точки, в яких можна побудувати тільки одну дотичну площину до поверхні. Особливими точками поверхні вважаються ті, в яких не можна побудувати тільки одну дотичну площину. Прикладами особливих точок поверхні є: вершина конуса, точка ребра повернення і т.д. дотична площину в яких може бути однозначно не визначена, тобто може бути проведено безліч площин.
Дотичні площини застосовуються при побудові ліній перетину поверхонь, при побудові нарисів поверхонь, при побудові власних тіней поверхні, при побудові нормалі до поверхні і т.д.
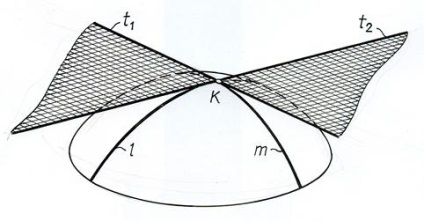
Для того, щоб провести пряму, дотичну до поверхні в певній її точці, досить через цю точку провести на поверхні будь-яку криву і побудувати дотичну пряму до неї. Оскільки через одну точку поверхні можна провести безліч кривих ліній, то в одній точці поверхні можна провести і безліч дотичних прямих.
Всі ці дотичні будуть лежати в одній площині, що є дотичною площиною до поверхні.
Таким чином, дотична площину до поверхні - це геометричне місце прямих, що стосуються даної поверхні в звичайній точці.
Щоб задати дотичну площину, досить побудувати дві дотичні прямі до поверхні.
Дотичній до поверхні називається пряма, яка є дотичною до будь-якої лінії, що належить цій поверхні.
Як лінії поверхні зазвичай використовуються лінії її визначника або лінії, які можуть бути легко побудовані графічно. Наприклад, у поверхонь обертання це паралелі і меридіани, у лінійчатої поверхні - її прямолінійні утворюючі.
Дотична площину може мати з поверхнею тільки одну спільну точку. В цьому випадку всі лінії поверхні, пересічні в даній точці, знаходяться по одну сторону від дотичної площини. Такі точки поверхні називаються еліптичними. Поверхні, у яких всі крапки еліптичні, є опуклими криволінійними поверхнями. До них відносяться сфера, еліпсоїд обертання, параболоїд обертання, закритий тор і т. Д.
Дотична площину може мати з поверхнею загальну лінію (пряму або криву). Наприклад, дотична площину стосується торсових поверхонь уздовж їх утворює - прямий лінії. Вона є дотичною площиною для всіх його точок, що лежать на цій прямій. Точки поверхні, що задовольняють цій умові, називаються параболічними. До них відносяться точки розгорнутих прямолінійних поверхонь - конічних, циліндричних і з ребром повернення.
Дотична площину до поверхні в даній точці може перетинати поверхню, до якої вона проведена. У перетині можуть виходити пересічні дві прямі, дві криві, або пряма і крива лінії.
Точки поверхні, дотична площину в яких перетинає поверхню, називаються гіперболічними. Такі точки дотику знаходяться на внутрішній поверхні відкритого тора.
Можливі такі основні випадки побудови дотичних площин до поверхонь:
1. через точку на самій поверхні
2. через точку, що лежить поза поверхні
3. паралельно заданої прямої
4. паралельно заданій площині
5. через пряму, що лежить поза поверхні
Побудова дотичної площини може виконуватися декількома способами:
1) побудовою двох дотичних прямих до двох кривих лініях поверхні (зазвичай для еліптичних точок дотику)
2) побудовою дотичного сліду площини до однойменного сліду поверхні
3) побудовою допоміжних перетинів поверхні з подальшим проведенням до них дотичних прямих певного напряму
Останні два способи застосовуються зазвичай для гіперболічних і параболічних точок дотику.
Розглянемо приклади розв'язання задач різних випадків.