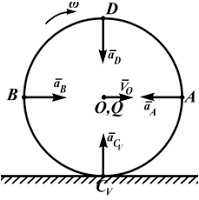
У навчальній літературі доводиться, що при русі фігури в площині в кожен момент часу існує така точка плоскої фігури, прискорення якої в цей момент дорівнює нулю.
Цю точку називають миттєвим центром прискорень (МЦУ). У наших міркуваннях будемо позначати її буквою Q
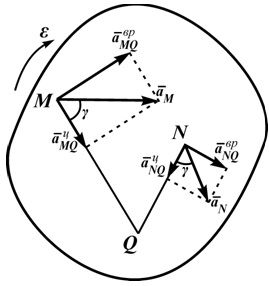
Взявши цю точку за полюс, отримаємо формулу для визначення прискорення довільної точки:
Кут, який складає вектор прискорення точки M з лінією MQ. визначиться зі співвідношення:
Тобто у всіх точок плоскої фігури цей кут однаковий.
З малюнка 2.23 видно, що миттєвий центр прискорень лежить в точці перетину ліній, складових кут γ з відповідними ускорениями точок.
На малюнках 2.24 - 2.26 наведені окремі випадки визначення положення миттєвого центру прискорень.