4.7.1 Ексцентриситет гіперболи
Ексцентриситетом гіперболи називається відношення полуфокального відстані до дійсної півосі і позначається.
Фокальними радіусами точки М гіперболи називаються відрізки прямих, що з'єднують цю точку з фокусами і.
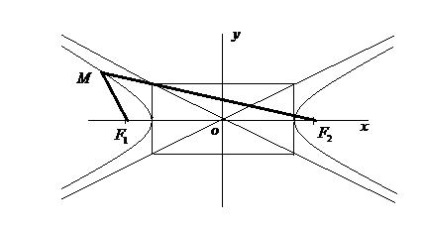
Оскільки гіпербола має дві гілки, то розділяють фокальні радіуси точок правої і фокальні радіуси точок лівої гілок (рис. 31, 32).
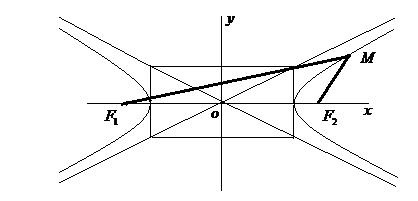
Фокальні радіуси точки М правійгілки гіперболи (рис.31) обчислюються за формулами
Фокальні радіуси точки М лівої галузі гіперболи (рис.32) обчислюються за формулами
4.7.3 директриса гіперболи
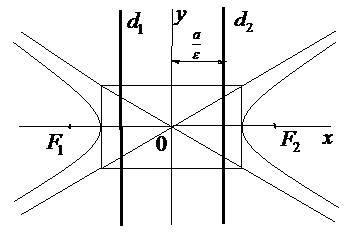
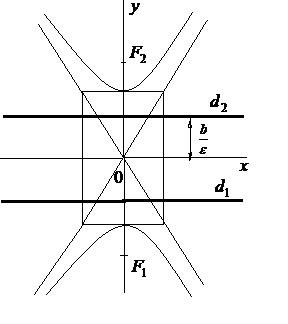
Директрисами гіперболи називаються прямі паралельні уявної осі і віддалені від неї на відстань. якщо (F1, F2) ОХ і. якщо (F1, F2) ОУ.
або (рис. 34) (4.8.1)
Директриси позначаються (ріс.33,34)
Дотичній до гіперболи в точці М0 називається граничне положення січної М0 М при М М0 по гіперболі.
Рівняння дотичних до гіперболи в точці ():
Пряма проходить через середини паралельних хорд гіперболи, називається її діаметром.
Всі діаметри гіперболи проходять через її центр (рис.35, 36)
4.8Решеніе завдань на визначення основних елементів гіперболи
Завдання 29 Знайти піввісь, координати фокусів і ексцентриситет гіперболи, заданої рівнянням. Обчислити довжини фокальних радіусів точки.
1 Запишемо канонічне рівняння гіперболи, розділивши обидві частини на 20, отримаємо
2 Знайдемо піввісь гіперболи
3 Знайдемо координати фокусів гіперболи
- Знайдемо ексцентриситет гіперболи
Фокуси еліпса лежать на осі ОХ, тоді скористаємося формулою (9)
- Обчислимо довжини фокальних радіусів
Оскільки точка М лежить на лівій гілці гіперболи, то при обчисленні і
необхідно скористатися формулами (10.1)
Завдання 30 Записати рівняння асимптот і директрис гіперболи
1 Запишемо канонічне рівняння гіперболи, розділивши обидві частини на 36, отримаємо
2 Знайдемо піввісь гіперболи
3 Складемо рівняння асимптот за формулами (7)
4 Складемо рівняння директрис
За формулою (9) знайдемо ексцентриситет гіперболи
За формулою (11) складемо рівняння директрис
Відповідь: рівняння асимптот. ,