Основне завдання кінематики точки полягає в розробці способів завдання руху точки і методів визначення основних кінематичних характеристик руху.
Основне завдання кінематики твердого тіла полягає в розробці способів завдання руху і методів, що дозволяють на основі невеликого числа характеристик, спільних для всіх точок знаходити кінематичні характеристики кожної точки тіла.
Задати рух точки, значить вказати математичний апарат, за допомогою якого в будь-який заданий наперед момент часу визначити положення точки в просторі.
3. Векторний, координатний і природний спосіб завдання руху точки
Задати рух точки, значить задати математичний апарат, за допомогою якого можна в будь-який заданий наперед момент часу визначити положення точки в просторі.
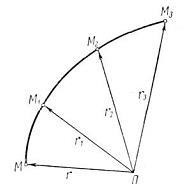
З плином часу точка змінює своє положення в просторі тіла відліку. Тому радіус-вектор змінюється як за напрямком, так і за величиною і являє собою деяку векторну функцію скалярного аргументу t. . Якщо функція задана або відома, то мова йде про векторному способі завдання точки.
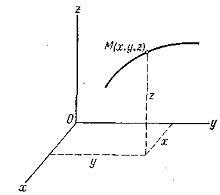
Якщо функції відомі або задані, то мова йде про координатном способі завдання руху.
Нехай нам відома траєкторія руху точки. На цій траєкторії вибираємо довільну точку О. Положення точки М на траєкторії можна задати за допомогою дугового координати.
З плином часу дугова координата змінюється і є деякою функцію Якщо функція задана мова йде про природному способі завдання руху точки.
4. Визначення швидкості і прискорення при векторному способі завдання руху.
При векторному способі завдання руху положення рухається точки в кожен момент часу визначається радіус-вектором який є функцією часу При переміщенні точки її радіус-вектор нього бере зріст. Ставлення вектора переміщення до проміжку часу. протягом якого відбувається це переміщення, являє собою вектор середньої швидкості руху точки:.
Вектор швидкості точки в даний момент часу дорівнює похідною від радіус-вектора точки по часу:
Вектор швидкості точки спрямований по дотичній до траєкторії в сторону руху точки.
Припустимо, що в початковий момент точка має швидкість. а через деякий час від нього бере зріст. Розділивши приріст на проміжок часу. отримаємо вектор середнього прискорення цієї точки за цей проміжок часу. Вектор прискорення точки дорівнює першої похідної від швидкості або другій похідній від радіус-вектора точки по часу.
Вектор прискорення спрямований по дотичній до годографу швидкості - геометричному місцю кінців векторів швидкості рухається точки, відкладених від однієї і тієї ж довільної точки простору.
5. Визначення швидкості і прискорення при координатному способі завдання руху точки
Нехай задані рівняння руху точки:
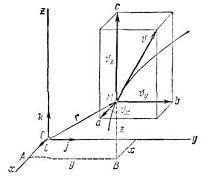
Обчисливши проекції швидкості на осі декартових координат, можна визначити модуль і напрям вектора швидкості за такими формулами:
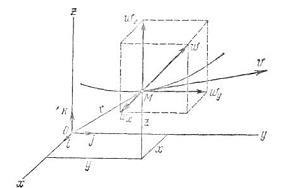
Обчисливши проекції прискорення на координатні осі можна визначити модуль і напрямок прискорення за такими формулами:
6. Визначення швидкості і прискорення при природному способі завдання руху точки
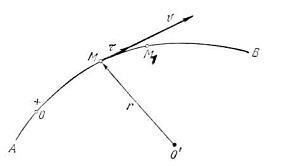
Домовимося алгебраїчну величину швидкості позначати символом. а модуль швидкості - буквою. тоді:
тобто модуль швидкості дорівнює абсолютному значенню похідної від дугового координати точки за часом.
Проекція прискорення точки на дотичну дорівнює другій похідній від дугового координати точки за часом або першої похідної від алгебраїчної величини швидкості точки за часом.
Поступальний рух тіла. Завдання руху. Розподіл швидкостей і прискорень точок тіла
Поступальним рухом твердого тіла називається такий рух, при якому будь-яка пряма, що з'єднує дві точки тіла, рухається паралельно самій собі.
Теорема. Всі точки твердого тіла, що рухається поступально, описують однакові (що збігаються при накладанні) траєкторії і в кожен момент часу мають геометрично рівні швидкості і прискорення.
Рівняннями поступального руху твердого тіла є рівняння руху будь-якої точки цього тіла - зазвичай рівняння руху його центра ваги:
Загальні для всіх точок твердого тіла, що рухається поступально, швидкість прискорення називають швидкістю і прискоренням поступального руху твердого тіла.
Обертальний рух. завдання руху
Обертальним називається такий рух тіла, при якому залишаються нерухомими всі його точки, що лежать на деякій прямій, званої віссю обертання.
При цьому русі всі інші точки тіла рухаються в площинах перпендикулярних осі обертання, і описують кола, центри яких лежать на цій осі.
При обертанні тіла кут повороту змінюється в залежності від часу:.
Величина, що характеризує швидкість зміни кута повороту з плином часу називається кутовою швидкістю тіла.
Величина, що характеризує швидкість зміни кутової швидкості з плином часу, називається кутовим прискоренням тіла.
Рівняння рівномірного обертання тіла. Обертання тіла з постійною швидкістю називається рівномірним.
Рівняння равнопеременное обертання тіла. Обертання тіла, при якому кутове прискорення постійно, називають равнопеременное обертанням.