Розглянемо ознаки катастроф. Про наявність катастрофи свідчать спеціальні критичні точки сімейства потенційних функцій, якими описується система або явище. Однак такі точки часто не можуть бути розпізнані відразу.
Наприклад, потенційна функція є дуже складною або точно не відома. Ще гірше, коли система не є градиентной, і зовсім погано, коли немає навіть туманних міркувань про вид рівняння, адекватно тому, що описує систему.
Однак, катастрофи часто зустрічаються в реальних ситуаціях, і, отже, важливо вміти їх вчасно розпізнати. Катастрофи мають відмінні риси - ознаки, які дозволяють привернути увагу до даного процесу.
Як тільки зафіксовано один з них, тобто встановлена ознака, що свідчить про наявність в системі катастрофи, керуючі параметри системи можна змінювати так, щоб знайти і інші ознаки, які при відповідних умовах повинні обов'язково виявитися. Встановлення наявності і типу катастрофи в разі невизначеності в описі системи допомагає визначити:
- спрощену модельну потенційну функцію, залежну тільки від істотних змінних стану і керуючих параметрів;
- структурно стійку частину потенційної функції, яка може підказати, який фактично має місце;
- тип рівняння для системи і те, яким чином потенційна функція в нього входить;
- непотрібність використання рівнянь взагалі.
Опис ознак катастроф
модальність
Система може мати два або більше різних станах в деякій області зміни керуючих параметрів. Наприклад, якщо керуючі параметри системи перебувають в заштрихованої області, то система може перебувати в трьох різних станах (наприклад, катастрофа збірки на рис. 1).
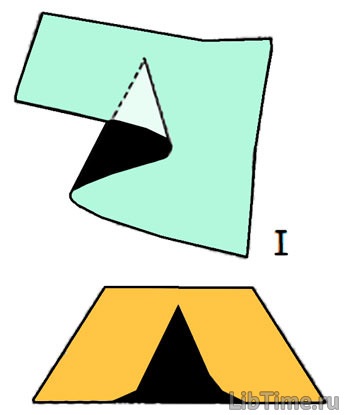
Малюнок 1 - Модальність і недосяжність в катастрофі збірки
недосяжність
Існує область недосяжних нестійких станів рівноваги, якої не можна прийти, рухаючись з яких-небудь стійких станів. На рис. 1 серединний шар є недосяжним.
катастрофічні скачки
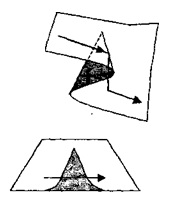
Малюнок 2 - Катастрофічні скачки
Малі зміни в значеннях керуючих параметрів можуть викликають великі зміни в значеннях змінних стану системи в міру того, як система перескакує з одного локального мінімуму в інший, перехід з околиці одного локального мінімуму в інший виявляється у великій зміні значень зміною стану, яке відбувається в надшвидкої шкалою .
На рис. 2 стрибок відбувається, як тільки стан системи переходить з одного шару поверхні катастрофи збірки на інший.
розбіжність
Кінцеві зміни в значенні керуючих параметрів призводять до кінцевих змін в значеннях змінних стану в точці рівноваги.
Зазвичай малі зміни в початкових значеннях керуючих параметрів ведуть лише до невеликої зміни початкових і кінцевих значень змінних стану. Однак при наявності катастрофи малі зміни початкових значень змінних стану можуть привести до великих змін кінцевих значень цих змінних.
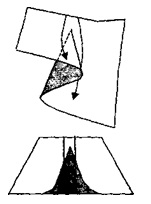
Малюнок 3 - Розбіжність
На рис. 3 показано, що траєкторії зміни керуючих параметрів при близьких початкових станах системи призводять до істотної відмінності кінцевих станів системи.
Гістерезис і незворотність
Гістерезис має місце, коли процес не є повністю оборотним. Стрибок з локального мінімуму 1 в локальний мінімум 2 може не відбутися при тих же значеннях керуючих змінних, хоча стрибок з точки 2 в точку 1 мав місце під час руху у зворотний бік.
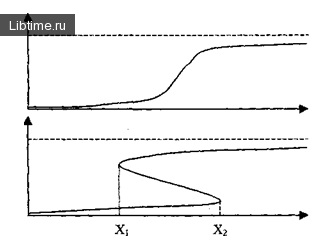
Малюнок 4 - Явище гістерезису
Розглянемо залежність ефективності праці робітника і винагороди. за яку він працює. Зі збільшенням винагороди ефективність праці також буде збільшуватися. Якщо винагорода не достатня, то працівник дуже старатися. З іншого боку, у кожного існує межа працездатності, і, як би не підвищувалася винагороду, більшого ефекту досягти не вдасться.
Ця ситуація приблизно може бути описана функцією, зображеною на рис. 4.
Розглянемо тепер динамічний процес, в якому оплата може підвищуватися і знижуватися. Якщо в початковий момент оплата низька, то ефективність роботи також низька. З підвищенням оплати ефективність зростає, але повільно, оскільки, на думку працівника, приріст оплати недостатній для збільшення ефективності роботи.
Так буде відбуватися до моменту Х2, коли подальше зростання оплати вимагає переходу на якісно новий рівень ефективності роботи. Відбувається стрибкоподібне зміна ефективності.
Якщо, навпаки, в початковий момент часу оплата висока, то ефективність підтримується на високому рівні. У зменшенням оплати відбувається поступове невелике зменшення ефективності (вступає в дію деяка інерція, згідно з якою людина продовжує працювати в звичному йому режимі).
Так відбувається до тих пір, поки оплата не досягне досить низького рівня Х1. У цей момент відбувається різке зниження ефективності, оскільки немає стимулів підтримувати її високий рівень. Фігура, зображена на рис. 4б, називається петлею гістерезису.
Строго кажучи, вона не є функцією, оскільки одному і тому ж значенню X може відповідати два (або навіть три) значення У. Наявність безлічі таких X - [Хр Х2] і призводить до можливості катастрофічних змін в стані системи. Саме безліч [Xt; Х2] називається бифуркационной безліччю. тобто такий, для значень параметрів з якої можливо кілька різних станів системи. На рис. 5 показано те саме явище в тривимірній системі.
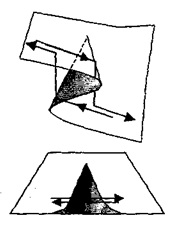
Малюнок 5 - Незворотність в тривимірній системі
Отже, катастрофою називається різке, стрибкоподібне зміна стану системи при повільному зміні її параметрів (або керуючих змінних).
Повертаючись до прикладу, можна помітити, що, якщо повернути осі і розглядати оплату як функцію ефективності, то ми маємо справу з поліномом третього ступеня (рис. 4). Цей поліном не має екстремумів, а на рис. 4б має два екстремуми. Очевидно, що кількість екстремальних точок залежати від коефіцієнтів полінома, тобто параметрів системи.
Розглянемо локальний характер потенційних функцій. Властивості станів рівноваги залежать від виду і властивостей потенційної функції, якій описується поведінка системи. Раніше розглядалася класифікація станів рівноваги в двовимірних системах, де виявилися можливими 8 різних варіантів рівноваги. Якщо ж змінних стану системи більше, то повна класифікація станів рівноваги виявляється дуже скрутній.
Теорія катастроф дозволяє провести таку класифікацію для досить широкого класу нелінійних систем.
Розглянемо, які перетворення можливі для потенційних функцій в околиці стану рівноваги. Ці перетворення дозволяють спростити процедуру і привести її до локально простого виду і виділити катастрофи.
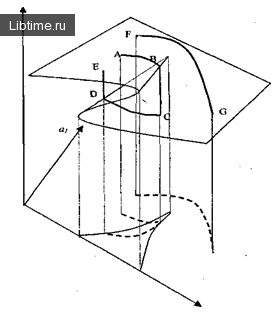
Малюнок 6 - Катастрофа збірки
Як видно з малюнка, система, починає свій рух з точки A, як можна довше рухатися по верхній частині поверхні, поки не досягне безлічі сингулярності в точці В. Потім система здійснює різкий стрибок вниз в точку С і піде по нижній частині поверхні.
Якщо система починає свій рух на нижній частині, то вона перетне біфуркаційні безліч в точці D і зробить різкий стрибок на верхню частину поверхні. Можлива і інша поведінка системи, яка не включає різких переходів. Наприклад, по траєкторії FG, якщо один з параметрів системи також може швидко змінюватися.
Економічні застосування теорії катастроф багато в чому спираються на геометричні аспекти, в основному для опису економічної поведінки застосовується саме катастрофа збірки. Інші елементарні катастрофи проілюструвати складно, оскільки в них необхідно закріплення одного або декількох параметрів.
Теорія катастроф застосовується для вивчення багатьох проблем, включаючи крах фондових бірж, поведінка уряду, макромоделі, структурні аспекти припущення Вальраса та ін ..