Паралельні і пересічні площині

Площині паралельні, якщо дві пересічні прямі в одній площині паралельні відповідним двом пересічним прямим в іншій площині, якщо площині не паралельні, то вони перетинаються (рис.16).

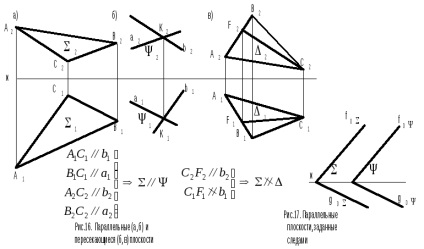
Площини, що перетинаються, утворюють лінію перетину площин. Для її побудови досить знайти дві загальні точки цих площин. Наприклад: дано дві площини -  (трикутник) і (пересічні прямиеa, b) (рис.18). Необхідно побудувати лінію їх перетину.

Р

ешеніем. Завдання вирішується за допомогою допоміжних площин, січних задані.

1

.Плоскості і перетинаються допоміжної фронтально проецирующей плоскостью. За фронтальним проекція ліній перетину плоскостей і (отрезок2),  і (отрезок1) будують їх горизонтальні проекції (отрезкі4 і3). Знаходять точкуК1 перетину цих горизонтальних проекцій. ТочкаК1 загальна для всіх трьох площин (,  і). На лінії зв'язку будують її фронтальну проекціюК2.

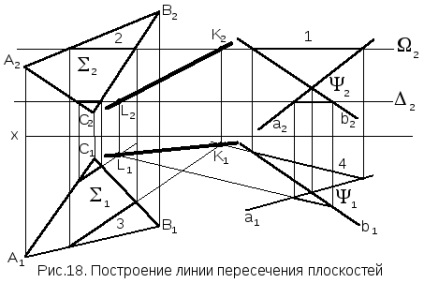
2.Плоскості  і перетинають допоміжною фронтально проецирующей плоскостью і повторюють вищеописані побудови. Знаходять другу загальну для трьох площин (,  і) точкуL (L1, L2 - її проекції). Пряма, що проходить через точкіK іL є лінія перетину площин.

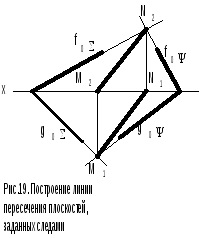
У разі, якщо площині  і  задані слідами (рис.19), то для побудови лінії перетину площин необхідно: 1. Продовжити следиі визначити точкіM1, N2 перетину однойменних слідів.

2. Побудувати на осі х відсутні проекції точок пересеченіяM2, N1.

3. З'єднати фронтальні і горизонтальні проекції точок M1N1 іM2N2. Лінія, що проходить через точкіM, N є лінією перетину площин.

Взаємне положення точки і площини, прямої і площини.

Точка належить площині. якщо через неї можна провести пряму, що лежить в цій площині.

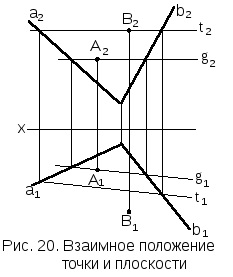
Завдання. Дано: пересічними прямими a, b задана площина. Є дві точки пространстваА, В. Необхідно з'ясувати яка з точок належить площині.

Рішення (рис.20). 1. Через фронтальні проекції точок А, В проводять фронтальні проекції горізонталейg2, t2 площині.

2. Будують горизонтальні проекції горизонталей g1, t1. Якщо проекції точки лежать на однойменних проекціях горизонталей, то точка належить площині (в прикладі - Точкан), якщо хоча б одна проекція точки не лежить на однойменній проекції горизонталей, то точка не належить площині (в прикладі - Точкан).

Пряма може належати площині, бути їй паралельна і перетинати її. Пряма належить площині, якщо дві її точки

належать даній площині. Звідси випливає правило: пряма лежить в площині, якщо вона перетинає дві прямі, що належать площині. На рис.21, а показана прямаяKL належить плоскості (АВС), оскільки прямаяKL перетинає прямиеАВ ІТТ. належать плоскості.

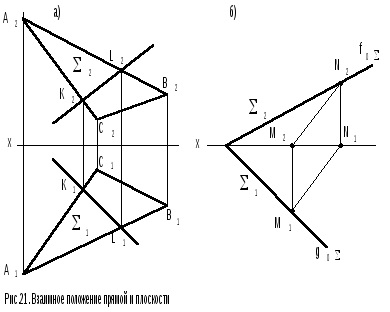
Якщо площину задана слідами, то правило звучить так (рис.21, б): пряма (сліди М1, N2) належить площині (), якщо сліди прямої лежать на однойменних слідах площині.

Прямі (в площині) особливого положення: 1) горизонталь площини; 2) фронталь площини; 3) профільна пряма площині; 4) лінія найбільшого скату.

Горизонталь площини - це пряма, що лежить в площині і паралельна горизонтальній площині проекцій. Фронталь і профільна пряма - це прямі, що лежать в площині і паралельні відповідно площинах проекційП2 іП3 .Лінія наібольшегоската - це пряма, що лежить в площині і перпендикулярна горизонталях площині.

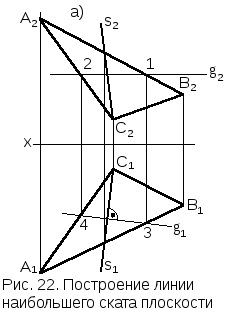
Завдання. Дано: площину задана трикутником АВС. Необхідно побудувати лінію її найбільшого ската.

Рішення (рис.22). 1. На площині проекцій П2 будується фронтальна проекція довільної горізонталіg2 (паралельно осіх), потім її горизонтальна проекціяg1 (точкі3, 4).

3. Перпендикулярно g1 з будь-якої точки площини (в прімереС1) проводиться горизонтальна проекція лінії найбільшого скатаs1. На фронтальній проекції будується її фронтальна проекціяs2.

По лінії найбільшого скату визначають кут нахилу площини до горизонту, який ще називається кутом падіння площини.

Пряма паралельна площині. якщо вона паралельна будь-якої прямої, що лежить у цій площині.

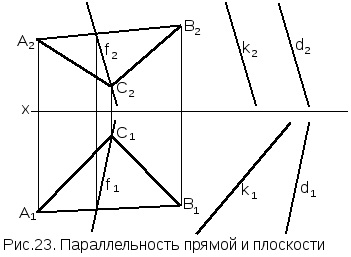
Завдання. Дано (рис.23): трикутником АВС задана площина. Прямиеk, d. які не належать площині. Визначити яка з прямих паралельна площині.

Рішення. 1. У фронтальній проекції будують проекцію f2 прямойf. що належить плоскостіАВС і паралельну проекція даних прямихk2 іd2.

2. Будують горизонтальну проекцію f1 прямойf. Якщо однойменні проекції даної прямий і прямий, що належить площині паралельні, пряма паралельна площині (в прімереd // АВС). Якщо хоча б одна проекція не паралельна, то пряма не паралельна площині (в прімереk не паралельна плоскостіАВС).

Пряма перетинає площину. якщо вона їй не паралельна. В цьому випадку можна знайти точку перетину прямої з площиною.

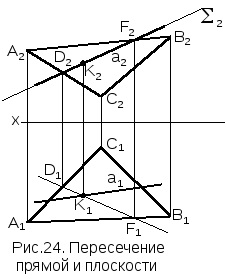
Завдання. Дано (рис.24): трикутником АВС задана площина, прямаяa. не паралельно площині. Визначити точку перетину прямої і площини.

Рішення. 1. Через пряму a проводять допоміжну плоскость. пересекающуюАВС. Доцільно використовувати проецирующую площину (в прикладі фронтально проектує). Плоскості іАВС у фронтальній проекції перетинаються по прямойD2F2. Будують її горизонтальну проекціюD1F1.

2. Визначають на горизонтальній проекції точку K1 перетину прямойа1 іD1F1. яка є горизонтальною проекцією точки перетину прямойа і плоскостіАВС. Будують фронтальну проекціюK2 точкіК.

Окремий випадок перетину прямої і площини - це їх взаємно перпендикулярність. Пряма перпендикулярна площині, якщо вона перпендикулярна двом пересічним прямим, лежачим в цій площині. Як пересічних прямих зручно вибирати прямі приватного положення: горизонталь і фронталь. Тоді правило перпендикулярності прямої і площини звучить так: пряма перпендикулярна площині, якщо її горизонтальна проекція перпендикулярна до горизонтальної проекції горизонталі площини, а фронтальна проекція прямої перпендикулярна до фронтальної проекції фронталі площині.

З

Адачі. Дано (рис.25, а): треугольнікомАВС задана площина, поза нею знаходиться точкаD. Необхідно з точкіD опустити перпендикуляр на плоскостьАВС.

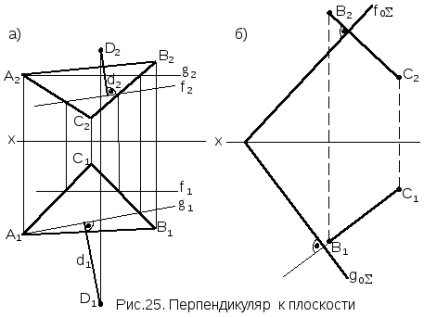
Рішення. 1. Будують горизонталь g і фронтальf плоскостіАВС.

2. З точок D1, D2 опускають перпендикуляри на відповідні проекції фронталіf2 і горізонталіg1. Прямаяd є перпендикуляр до плоскостіАВС.

Якщо площину задана слідами, то епюр прямий ВС перпендикулярної плоскості виглядає як на рис. 25, б.

Схожі статті

• Перетин двох площин-ілюстрований самовчитель по створенню креслень-оглядач навчальних