Перетин кулі площиною
Теорема 20.3. Будь-яке перетин кулі площиною є коло. Центр цього круга є підстави перпендикуляра, опущеного з центра кулі на січну площину.
Доведення. Нехай - січна площина і Про - центр кулі (рис. 453). Опустимо перпендикуляр з центру кулі на площину і позначимо через О 'підставу цього перпендикуляра.
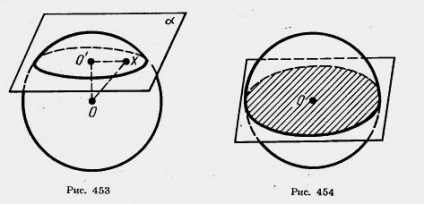
Нехай X - довільна точка кулі, що належить площині. По теоремі Піфагора 0X 2 = 00 '2+ О'Х 2. Так як ОХ не більш радіуса R кулі, то. т. е. будь-яка точка перетину кулі площиною знаходиться від точки О 'на відстані, що не більше. отже, вона належить колу з центром О 'і радіусом.
Зворотно: будь-яка точка X цього кола належить кулі. А це означає, що перетин кулі площиною є коло з центром в точці О '. Теорема доведена.
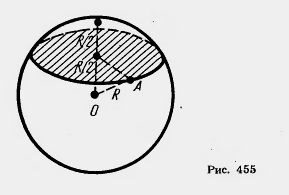
Площина, що проходить через центр кулі, називається діаметральної площиною. Перетин кулі діаметральної площиною називається великим колом (рис. 454), а перетин сфери - великий окружністю.
Завдання (30). Через середину радіуса кулі проведено перпендикулярна йому площину. Як відноситься площа отриманого перерізу до площі великого кола?
Рішення . Якщо радіус кулі R (рис. 455), то радіус кола в перерізі буде
.
Відношення площі цього кола до площі великого кола одно
А. В. Погорєлов, Геометрія для 7-11 класів, Підручник для загальноосвітніх установ
Якщо у вас є виправлення або пропозиції до даного уроку, напишіть нам.
Якщо ви хочете побачити інші коригування та побажання до уроків, дивіться тут - Освітній форум.