Єдина вимога, що пред'являється до чисел, службовцям шкальними значеннями, полягає в тому, що розглядають-Ріва емпіричні відносини повинні переходити в відпо-ціалу їм числові відносини. Цієї вимоги, як правило, буває недостатньо для однозначного визначення безлічі шкальних значень. Сукупності величин, отриманих за викорис-зуемое в соціології шкалами, зазвичай бувають визначені лише з точністю до деяких перетворень цих величин, які називаються допустимими перетвореннями відповідних шкал; У відповідності зі сформованою в літературі традицією тип шкали визначається відповідним цій шкалі безліччю допустимих перетворень.
Щоб пояснити введені визначення, опишемо типи найбільш часто використовуються в соціології шкал.
Шкали найменувань (номінальні, класифікаційні). При використанні шкали найменувань об'єкти вимірювання розпаду-ються на безліч взаємно виключають і вичерпних клас-сов. Кожному класу дається найменування, числове позначення якого є одним з шкальних значень. Шкала найменувань-ваний виходить, якщо в якості модельованих в процесі через виміри емпіричних відносин виступають лише відносини рівності і нерівності між об'єктами. Вимоги, що пред'являються-мі до шкальні значеннями, полягають у тому, що рівним об'єктів повинно відповідати одне і те ж число, а нерівним - різні числа. Тому номінальна шкала фактично задає деяку класифікацію вихідних об'єктів. Один клас - це сукупність об'єктів, що мають один і той же шкальної значення.
Номінальні шкали можна визначити як шкали, допустимими перетвореннями яких є довільні взаємно однозначні перетворення 3, т. Е. Перетворення, що зберігають відносини рівності і нерівності між числами. Досліджувані емпіричні відносини однаково добре будуть відображати, напри-заходів, такі сукупності шкальних значень: (1, 1, 2, 3, 4) і (15, 15, 14, 13, 12). Кожна з цих сукупностей отримана з іншої за допомогою деякого однозначного перетворення.
Однак вже тут проблема вимірювання (т. Е. Приписування респондентам певних чисел) не настільки проста. Не можна з предель-ної чіткістю виділити всілякі професії або, принаймні, вважати, що всі професії взаємно виключають одна одну. Наприклад, неминуче доведеться зіткнутися з таким приватним слу-чаєм, коли професія буде комбінацією декількох. І тоді постане питання про співвідношення респондента, що має таку про-професію, з деякою групою професій і позначенні її числовим знаком.
Порядкові шкали (шкали порядку). Порядкова шкала напів-чає, якщо при здійсненні вимірювання моделюються не тільки емпіричні відносини рівності і нерівності між вивчати-мимі об'єктами, по і відносини порядку між ними. Порядкова шкала не тільки задає деяку класифікацію на безлічі об'єктів, а й встановлює певний порядок між клас-самі.
Порядкові шкали можна визначити як шкали, як допустимих перетворень яких виступають довільні мо-Нотона зростаючі перетворення 4. Останні утворюють подсовокупности всіх взаємно однозначних перетворень, включаю-щую ті з них, які зберігають відношення порядку між числами. Прикладом сукупностей шкальних значень, отримую-трудящих одна з одної за допомогою деякого монотонно зростаючою-го перетворення, можуть служити сукупності (1, 3, 5, 4, 2) і (18, 20, 28, 24, 19). Цікавлять нас відносини рівності, що не-рівності і порядку між об'єктами з однаковим успіхом відпрацьовано-дружини в будь-який з цих сукупностей. Ясно, що порядкові шкали утворюють підмножину номінальних шкал.
Приклад порядкової шкали ми отримаємо, якщо будемо розрізняти людей даної професії по кваліфікації (складності праці і т.д.).
На практиці часто не вдається повністю упорядкувати об'єкти досліджуваної сукупності щодо того чи іншого інтересующе-го дослідника властивості. Припустимо, наприклад, що вивчається сукупність людей носіїв властивості - «задоволеність спеціальністю», а вужче - властивості, що міститься в питанні «Чи задоволені Ви своєю спеціальністю?» І п'яти відповідях на нього від «повністю задоволений» до «зовсім не задоволений ». Зазвичай вважається, що будь-яку сукупність людей можна уперед-чить щодо даної властивості, т. Е. Що відповіли «спеціальністю повністю задоволений» вище за измеряемому якості, ніж ті, хто відповів, що «спеціальністю задоволений» і т. Д. найчастіше передбачуваного чіткого розрізнення оцінок не спостеріга-дається і респонденти не можуть однозначно вибрати ту чи іншу відповідь. У цьому випадку на допомогу можуть прийти частково уперед-ченние безлічі.
Шкальні значення, отримані по порядкової шкалою, часто називають рангами.
Інтервальні шкали (шкали інтервалів). Інтервальні шкали виходять, якщо в процесі вимірювання ми моделюємо не тіль-ко ті відносини, які моделюються при використанні поряд-кової шкали, але і ставлення рівності (або, що одне і те ж, порядку) для різниць (інтервалів) між досліджуваними об'єктами. Далеко не завжди в тих випадках, коли вдається побудувати близько-ву шкалу, вдається побудувати і интервальную. Наприклад, візьмемо класифікацію робочих по розрядам. Відомо, що перший розряд нижче другого, другий - третього і т. Д. (І це відповідає визна-поділеній емпіричному відношенню порядку між респондентами), т. Е. Розряди відповідають порядкової шкалою. Однак зіставляти дистанції між кожною парою розрядів все ж не можна.
Інтервальним шкалами відповідають позитивні лінійні перетворення 5, т. Е. Такі перетворення, які, поряд з від-відносинами рівності, нерівності та порядку між числами со-зберігаючі та відносини рівності і порядку між їх дивовижними речами, (або, що те ж саме, приватна від ділення будь-якої такої різниці на будь-яку іншу). Прикладом сукупності чисел, які утворюються одна з одної за допомогою позитивного лінійного Перетворюва-ня (У = 3х + 9), служать сукупності (5, 5, 2, 1, 2) і (24, 24, 15, 12, 15). Неважко перевірити, що в цих сукупностях відображаються одні і ті ж відносини рівності, нерівності та порядку, як для чисел, так і для інтервалів між ними (так, для першої сукупність-ності 5 - 2> 2 - 1, а для відповідних шкальних значень з другої сукупності 24 - 15> 15 - 12). Легко бачити також, що приватні від розподілу величини одного інтервалу між шкальними значеннями на величину іншого не залежать від того, яку з розглянутих шкал ми вибираємо (так, правильне співвідношення (5 - 2) :( 2-1) = (24-15) : (15-12) = 3). Це справедливо для будь-яких інтервальних шкал. Ясно, що позитивні лінійні перетворення є-ються під сукупністю монотонно зростаючих перетворень, а сукупність інтервальних шкал - підмножиною шкал порядку.
Головні труднощі при побудові інтервальних шкал в соціології полягає в обґрунтуванні рівності або різниці дистанцій між об'єктами. Процедури, що дозволяють таким чином перетворити шкальні значення порядкової шкали, що рівність (порядок) відстаней між отриманими числами можна буде трактувати як відображення відповідного рівності (порядку) «відстаней», між досліджуваними об'єктами, звуться метризації шкали (або «оцифровки» шкальних значень.) 6. На практиці через вестно багато методів шкалювання, що дозволяють отримувати ін-тервальную шкалу «непрямим» чином, без відображення вказано-ного відносини безпосередньо в процесі вимірювання 7.
Шкалами відносин відповідають позитивні перетворення подібності 8, складові подсовокупности позитивних чи-лінійних перетворень, які залишають без зміни ставлення між числами (під ставленням тут розуміється частка від де-лення одного числа на інше). Шкалу відносин отримаємо, якщо будемо вимагати, щоб в процесі вимірювання не тільки відносини між емпіричними об'єктами відображалися в відповідні; числові відносини, але і один і той же об'єкт відображався в 0. Подібна можливість іноді виникає в соціологічних дослі-нях. Так, при вивченні задоволеності респондентів своєю працею, ймовірно, в якості такого об'єкта має, сенс вибрати респондента, байдужого до своєї роботи. Фіксацію такого нулі-вого об'єкта можна розглядати як завдання початку відліку; шкальних значень. Тому можна сказати, що шкали відносин утворюють підмножину інтервальних шкал, що характеризується фіксацією початку відліку. Неоднозначність сукупності шкальних; значень, отриманих за допомогою вимірювання за шкалою відносин, ілюструється прикладом наступних двох сукупностей, що відображає-чих одні і ті ж емпіричні відносини рівності, нерівності та порядку як між респондентами, так і між відповідними інтервалами і, крім того, що відповідають одному і тому ж початку відліку (один і той же об'єкт (другий) в обох випадках відображається в: (2, 0, -1,4, 1) і (3, 6, -3 / + 2, 6, 3/2). Легко бачити також, що для обох сукупностей приватні від розподілу між шкальними значеннями будь-яких пар об'єктів одні й ті ж (2: 4 = 3: 6 і т. д.). Ясно, що розглядаються сукупності виходять один з одного за допомогою деякого позитивного перетворення подібності (у = 3 / 2х). Шкали різниць - це шкали, яким відповідають перетворення зсуву 9. Ясно, що такі перетворення утворюють подсовокупности позитивних лінійних перетворень. шкали раз-ностей виходять з інтервальних шкал при фіксації одиниці виміру. Для більшості соціологічних шкал важко поставити природним чином таку одиницю (виняток становлять шка-ли типу «вік», «стаж роботи», «дохо »І деякі інші). Однак шкалу різниць можна отримати, наприклад, при знаходженні шкальних значень аналізованих об'єктів за допомогою неко-торих методів парних порівнянь (див. Гл. 7),
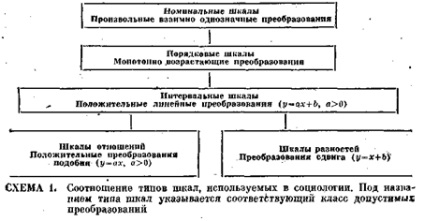
Сказане підсумовано в схемі 1, де вказані допустимі перетворення описаних шкал і відображено співвідношення їх типів.
Ознаки, значення яких отримані по порядкової або но-номінальної шкалою, зазвичай називають якісними, а ознаки, для отримання значень яких використовувалася шкала, тип кото-рій нижче типу інтервального шкали - кількісними.
Відповідно до наявної традицією будемо говорити, що дві шкали дозволяють досягти одного і того ж рівня вимірювання, якщо ці шкали є шкалами одного типу (т. Е. Якщо відповідними-ющие цими шкалами сукупності допустимих перетворень сов-падають) 1 0.