Функція називається періодичною функцією. якщо існує число. таке що вірно рівність
Графік періодичної функції має повторювані ділянки на кожному проміжку довжиною T. Найменше з чисел T називається найменшим періодом функції. За замовчуванням буквою Т позначають саме найменший період, (ріс.47).
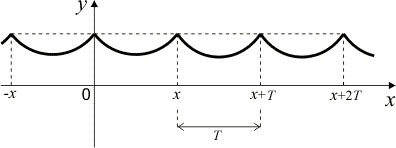
Дослідження періодичної функції і побудова її графіка слід проводити на проміжку, довжина якого дорівнює найменшому періоду функції; цей проміжок часто називають основним проміжком для періодичної функції.
Нижче перераховані деякі властивості періодичних функцій.
Періодична функція не може бути задана на безлічі, обмеженому зверху або обмеженому знизу.
Наприклад, функція. не є періодичною.
Якщо число є періодом функції. то число. де. також є її періодом.
Наприклад, функція. є періодичною, її найменший період і числа. також є її періодами.
Якщо число - це найменший період функції. то функція є також періодичної і її найменший період дорівнює числу.
Наприклад, функція. є періодичною і її найменший період дорівнює.
При складанні двох періодичних функцій з однаковими ООФ виходить періодична функція, причому її найменший період ділиться без остачі на і на. де. - це найменші періоди доданків.
Наприклад, - періодична с. - періодична з - періодична с. так як і.
Приклади (дослідження періодичності функцій)
1. Чи є функція періодичної? Чому дорівнює її найменший період?
Відомо, що основна елементарна функція є періодичною з найменшим періодом.
Перевіримо рівність для даної функції:
За виконання рівності робимо висновок, що дана функція є періодичною з періодом. Щоб знайти найменший період, знизимо ступінь вираження за відомою тригонометричної формулою:.
Тепер маємо суму двох періодичних функцій:
отже, дана функція має найменший період; тому досліджувати її властивості і будувати графік досить на основному проміжку, наприклад при. а потім зробити періодичне продовження на всю ООФ.
Відповідь: функція є періодичною з найменшим періодом.
2. Чи є функція періодичної?
Дана складна функція не є періодичною, так як не є періодичною її проміжна функція. "Спотворює" ті значення аргументу x. для яких однакові значення мала б функція.
Для ілюстрації сказаного перевіримо розташування нулів даної функції:
Маємо безліч всіх нулів функції:
Бачимо, що нулі функції розташовуються неперіодично на осі OX. Отже, ця функція не є періодичною (так як в іншому випадку все її властивості, в тому числі і нулі, повторювалися б періодично).
Відповідь: функція не є періодичною.
3. Вкажіть, які з наступних функцій є періодичними?
1) функція періодичної не є, так як рівність не виконується, наприклад, для точки. тому що точка через обмеженість знизу ООФ. (Рис.48);
2) функція періодичної не є, так як рівність не виконується, наприклад, для точки. (Ріс.49);
3) функція є періодичною з найменшим періодом. що добре видно по її графіку на рис. 50;
4) функція є періодичною з найменшим періодом. що добре видно по її графіку на рис. 51;
Відповідь: періодичними є тільки функції 3) і 4).