При підсумовуванні похибок керуються наступним:
1. Систематичні похибки -

2. Випадкові похибки, їх среднеквадратические оцінки підсумовують з урахуванням їх взаємних кореляційних зв'язків, грунтуючись на відомій з теорії ймовірностей залежності
(1.44) де
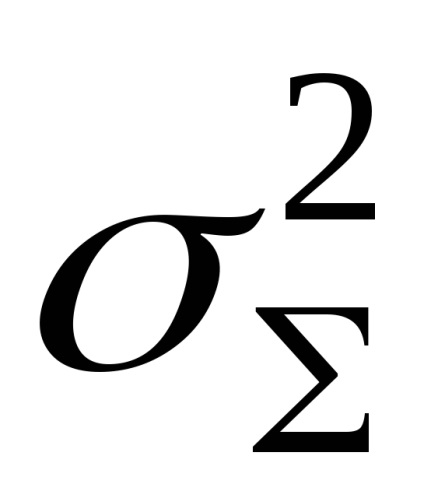
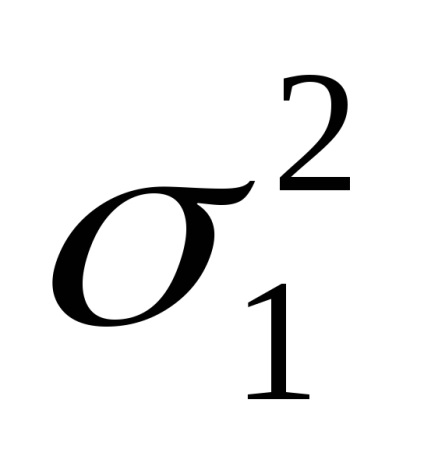
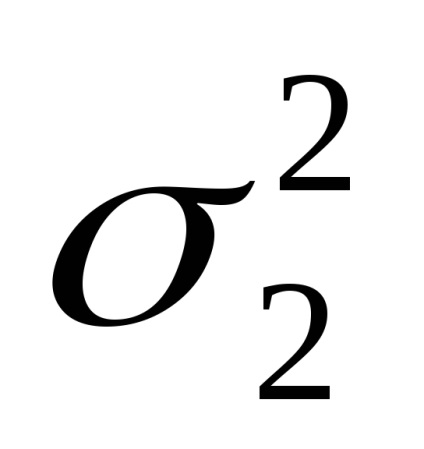
Сумарна середньоквадратичне похибка
Зазвичай інформація про міру кореляційних зв'язків відсутня, тому на практиці розглядають два крайніх випадки: r = 0, r = ± 1. Якщо r = 0, то випадкові похибки статистично незалежні (НЕ-корельовані), і похибки підсумовуються геометрично:
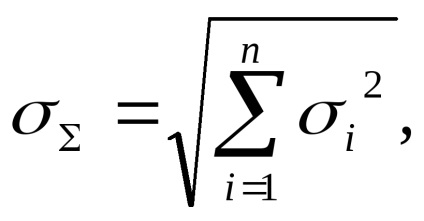
де

Якщо випадкові похибки жорстко корельовані (r = ± 1), то між результатами вимірювань існує функціональний зв'язок. У цьому випадку вони складаються, якщо r = + 1,
або віднімаються, якщо r = -1
Підсумовування систематичної похибки з випадковою здійснюють з урахуванням кореляційних зв'язків за тим же принципом, що і підсумовування випадкових похибок.
I.I3. Похибки непрямих вимірювань
При непрямих вимірах значення шуканої фізичної величі-ни знаходять шляхом узгоджених вимірювань інших величин, пов'язаних з вимірюваною величиною відомою функціональною залежністю. Ці інші величини будемо називати вимірюваними аргументами. Значення аргументів найчастіше знаходять в результаті прямих вимірювань, але іноді - в результаті спільних, сукупних або непрямих вимірювань. Тому виникає завдання: визначити похибки функції при даних погрішності аргументів.
Вимірюється величина Q пов'язана з вимірюваними аргументами залежністю
Зустрічаються випадки неявній залежності між Q і Qi.
По виду функціональної залежності розрізняють непрямі через виміри з лінійною залежністю між вимірюваноївеличиною і аргументами
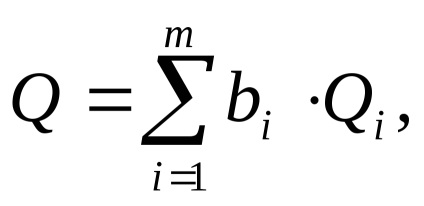
з нелінійної залежністю
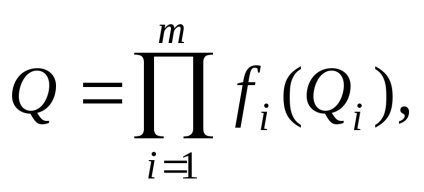
із залежністю змішаного типу
оцінимо результат
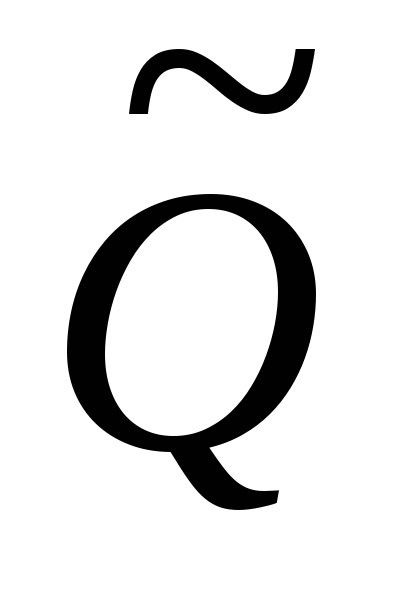
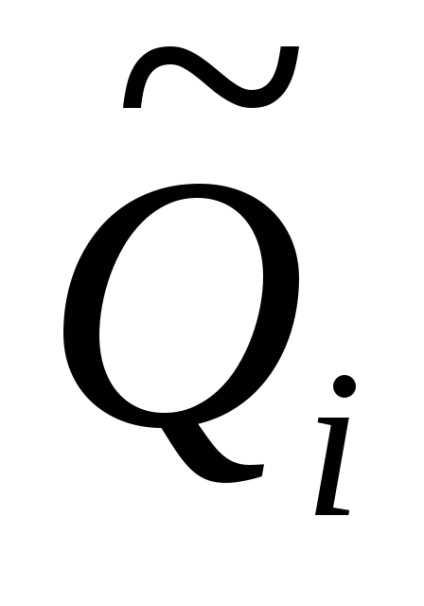
Нехай кожен з аргументів Qi характеризується оцінкою
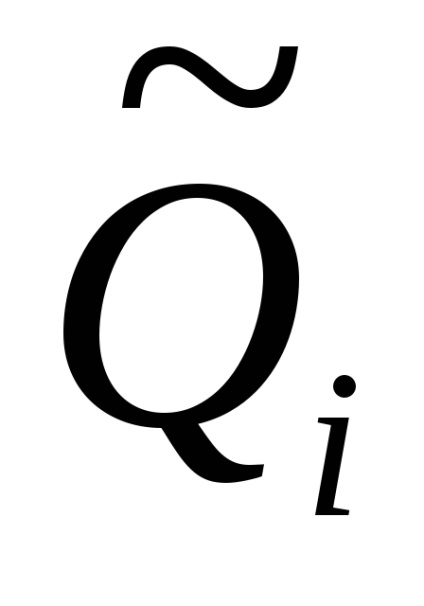
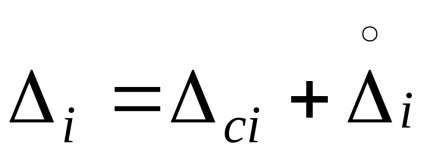
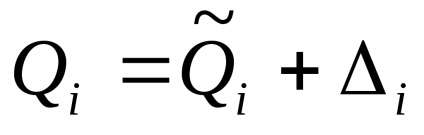
З рівняння (1. 49) отримуємо оцінку результату
і похибки непрямого вимірювання
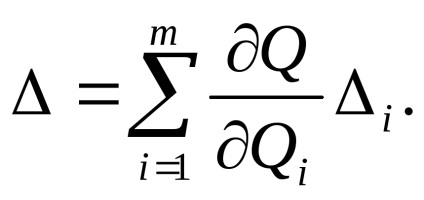
Допустимість такої оцінки повинна бути перевірена. похідні
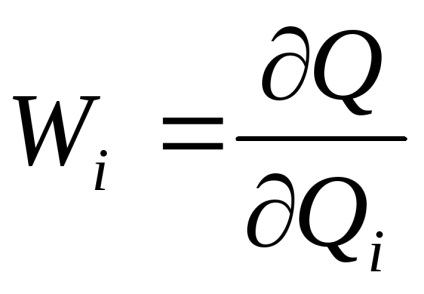
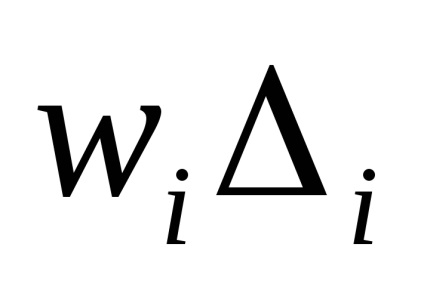
Розглянемо випадкові похибки. При цьому систематичні складові похибок оцінок всіх Qi будемо вважати постійні-ми. Висловимо оцінку середнього квадратичного значення випадкової похибки результату непрямого наміру як
де
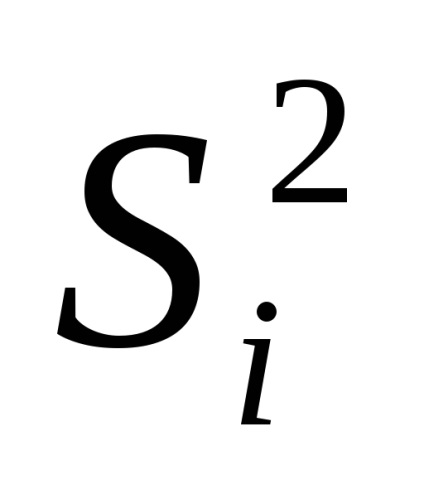
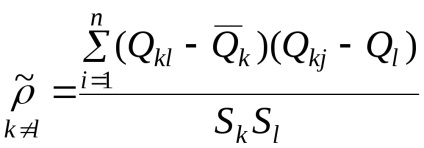
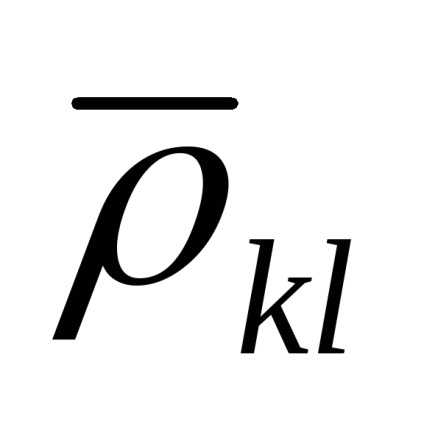
Коли вимірювання аргументів проводяться не одночасно, різними засобами вимірювань, то коефіцієнт кореляції близький до нуля, і
Введеним новим позначенням оцінки середнього квадратичного підкреслюється, що в рівняннях використовуються дисперсії результа-тов спостереження при прямих вимірах аргументів.
Постійна систематична похибка Δс результату косвен-ного вимірювання
Якщо знаки приватних систематичних похибок ci неіз-Вестн, то систематичну похибку результату непрямих изме-реній знаходять як
яку називають граничною.
При розрахунку відносних похибок сістсл вираження для с і
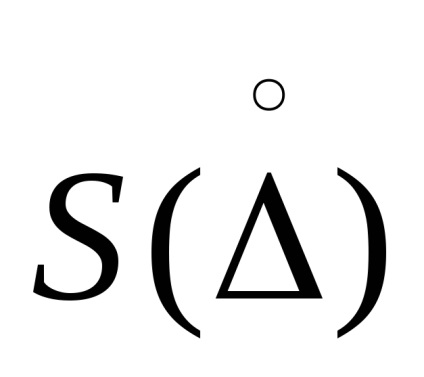
Слід зазначити, що відносна похибка непрямих через вимірювань в деяких випадках може набувати дуже великі зна-ня, наприклад, для функцією виду Q = Q1 -Q2 при малих значеннях різниці
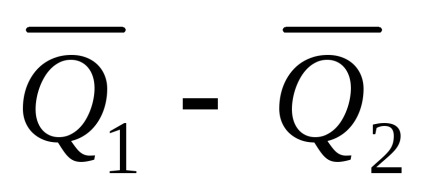
При непрямих вимірах необхідно розробляти такі мето-ди, які забезпечують збереження в допустимих межах похибкою-ності непрямого вимірювання. Це досягається вибором значень QlіQk. при яких відносна похибка не виходить за пре-дели допустимої; застосуванням способів вимірювання, при яких рівнян-ня непрямого вимірювання не містить малих різниць; разработ-кою методів і засобів вимірювань, що забезпечують пряме вимірювання замість непрямого.
Розглянемо, як оцінюється довірчий інтервал випадкової похибки і межі або довірчий інтервал не вилучених систематичних похибок результату непрямих вимірювань.
Випадкову похибку результату непрямого вимірювання мож-но вважати нормально розподіленої випадкової величиною навіть в тому випадку, якщо складові мають розподіл, відмінне від нор-мального, але число доданків не менше 4 -5 і відсутня Доміно-рующая похибка.
Довірчі кордону p випадкової похибки визначають за формулою
коефіцієнт
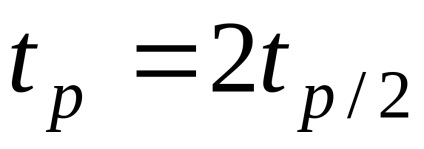
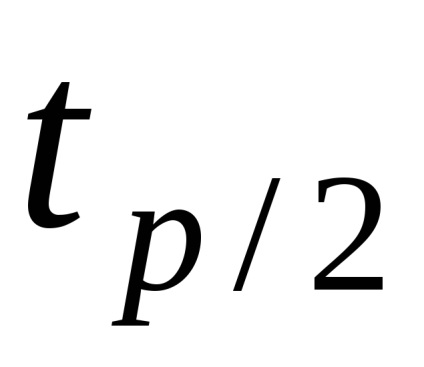
Як говорилося вище, не виключені систематичні похибкою-ності можна розглядати як величини випадкові. Для кожної зі складових знаходять кордону i і, якщо можливо обгрунтувати за-кон розподілу і оцінити
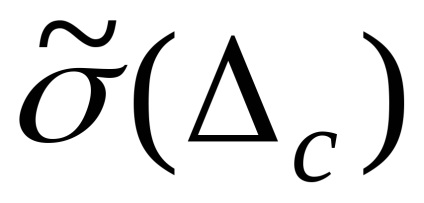
де k - коефіцієнт, який визначається прийнятою довірчою веро-ятность, який при довірчих ймовірності 0,9; 0,95; 0,99 приймають відповідно рівним 0,95; 1,1; 1,4.
Межі сумарної похибки вимірювань оцінюють відповідно до ГОСТ 8.207-76 [7].