Найдавнішими поняттями в розвитку світової геометрії є поняття площ багатьох прямолінійних фігур, в тому числі: прямокутника, паралелограма, трикутника, і трапеції. Ще в 7 столітті до нашої ери площа прямокутника вміли обчислювати єгиптяни. Вони множили довжину на ширину.
Вавилонська арифметика і алгебра теж були досить розвинені, про це свідчать знайдені під час розкопок клинописні таблички. Вавилонська геометрія мала уявлення про пропорційності відрізків, які перетиналися паралельними прямими, а також про теорему Піфагора і навіть обчисленні обсягів і площ деяких фігур. При цьому вавілоняни під просторовими фігурами брали конкретні предмети з побуту. Наприклад, при будівництві круглих будівель, вони довжину окружності приблизно вираховували за її трьом діаметрам. Площа прямокутника вони вираховували кількістю пройдених кроків. Мабуть для того часу такі визначення значень були цілком прийнятними. Така прикладна геометрія була характерна для багатьох народів світу і широко використовувалася у вирішенні різних спірних побутових питань.
Видатний вчений свого часу Архімед, доводячи теореми про площі фігур, використовував метод вичерпання. Насправді, це не що інше, як непрямий доказ, яке починають від противного. Основна ідея методу Архімеда полягає в тому, що всередину фігури, площа якої шукають, потрібно вписати правильні фігури. Використовуючи варіанти методу вичерпання, видатний вчений зміг довести багато теореми.
Теорема: площа прямокутника дорівнює добутку його суміжних сторін.
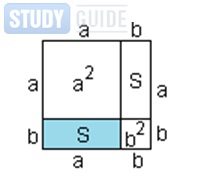
Перетворимо наш прямокутник в квадрат. Для цього збільшимо його сторону b до довжини сторони a
В результаті у нас вийшло чотири квадрати. Ми знаємо, що площа квадрата дорівнює (a + b) 2. У той же час ці квадрати складені з двох прямокутників: одного прямокутника з площею S і такого ж прямокутника з такою ж площею, а також двох квадратів, у яких площі a 2 иb 2. Виходячи з того, що наш чотирикутник складається не з одного чотирикутника, а з декількох, то його площа буде дорівнює сумі всіх площ даних чотирикутників. Це виходить з властивості площ:
(A + b) 2 = S + S + a 2 + b 2. або a 2 + 2ab + b 2 = 2S + a 2 + b 2.
А це означає, що S = ab.Значіт, наша теорема доведена.