Пряма лінія, що отримується при взаємному перетині двох площин, цілком визначається двома точками, з яких кожна належить обом площинам. Так, пряма K1 К2 (рис. 163), по якій перетинаються між собою площину, задана трикутником АВС, і пл. β, задана прямими DE і DF, проходить через точки K1 і K2; але в цих точках прямі АВ і АС першої площині перетинають пл. β т. е. точки К1 і К2 належать обом площинам.
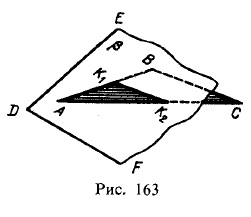
Отже, в загальному випадку для побудови лінії перетину двох площин треба знайти будь-які дві точки, кожна з яких належить обом площинам; ці точки визначають лінію перетину площин.
Для знаходження кожної з таких двох точок зазвичай доводиться виконувати спеціальні побудови. Але якщо хоча б одна з пересічних площин перпендикулярна до площини проекцій, то побудова проекцій лінії перетину спрощується. Почнемо з такої нагоди.
На рис. 164 показано перетин двох площин, з яких одна (задана трикутником DEF) розташована перпендикулярно до пл. π2. Так як трикутник DEF проектується на пл.π2 у вигляді прямої лінії (D "F"), то фронтальна проекція відрізка прямої, по якому перетинаються обидва трикутника, є відрізком К "1 К" 2 на проекції D "F". Подальша побудова ясно з креслення.
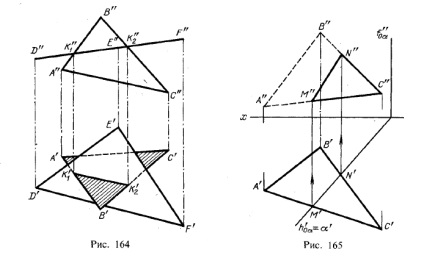
Інший приклад дан на мал. 165. Горизонтально-проектує площину α перетинає площину трикутника АВС. Горизонтальна проекція лінії перетину цих площин - відрізок M'N '- визначається на сліді α'.
Тепер розглянемо загальний випадок побудови лінії перетину двох площин. Нехай одна з площин, β, задана двома пересічними прямими, а інша, γ, - двома паралельними прямими. Побудова показано на рис. 166. В результаті взаємного перетину площин β і γ отримана пряма K1 K2. Висловимо це записом: β × γ = К1 K2.
Для визначення положення точок K1 і К2 візьмемо дві допоміжні фронтально-проектують площині (α1. І α2), що перетинають кожну з площин β і γ. При перетині площин β і γ площиною α1. отримуємо прямі з проекціями 1 "2", 1'2 'і 3 "4", 3'4'. Ці прямі, розташовані в пл. α1. в своєму перетині визначають першу точку, К1. лінії перетину площин β і γ.
Ввівши, далі, мул. α2. отримуємо в її перетині з β і γ прямі з проекціями 5 "6", 5'6 'і 7 "8", 7'8'. Ці прямі, розташовані в пл. α2. в своєму перетині визначають другу точку, К2. загальну для β і γ.
Отримавши проекції К'1 і К'2 знаходимо на слідах і α "1 і α" 2 проекції К "1 і К" 2. Цим визначаються проекції К'1 К'2 і К "1 К" 2 шуканої прямої перетину площин β і γ (проекції проведені штрихпунктирной лінією).
При побудові можна мати на увазі наступне: так як допоміжні січні площини α1 і α2 взаємно паралельні, то, побудувавши проекції 1'2 'і 3'4' слід для проекцій 5'6 'і 7'8' взяти по одній точці, хоча б 5 і 8, так як 5'6 '|| 1'2' і 7'8 '|| 3'4'.
У розглянутому побудові були взяті в якості допоміжних дві фронгально- проектують площині. Звичайно, можна було взяти і інші площини, наприклад дві горизонтальні або одну горизонтальну, іншу фронтальну і т. Д. Сутність побудов від цього не змінюється. Однак може зустрітися такий випадок. Покладемо, що були взяті в якості допоміжних дві горизонтальні площини і отримані при перетині ними
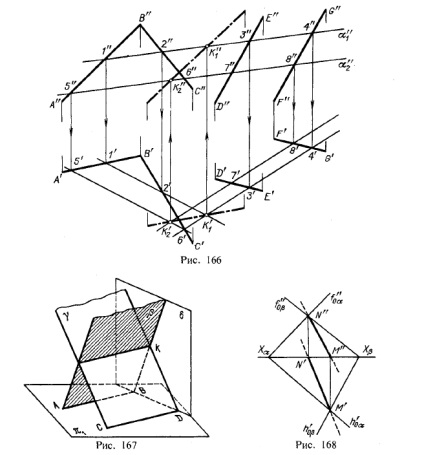
площин β і γ горизонталі виявилися взаємно паралельними. Але рис. 167 показує, що β і γ перетинаються між собою, хоча їх горизонталі паралельні. Отже, отримавши взаємно паралельні горизонтальні проекції горизонталей АВ і CD і знаючи, що площині при цьому не обов'язково паралельні, а можуть перетинатися (по загальній для них горизонталі), треба випробувати площині β і γ за допомогою хоча б, горізонгально-проецирующей площині (див . рис. 167); якщо прямі, за якими ця допоміжна площина σ, перетне β і γ, також виявилися б паралельні одна одній, то площини β і γ не перетинаються, а паралельні одна одній. На рис. 167 ці прямі перетинаються в точці К, через яку і проходить лінія перетину площин β і γ паралельно прямим ВА і CD.
Якщо площини задані їх слідами на площинах проекцій, то природно шукати точки, що визначають пряму перетину площин, в точках перетину однойменних слідів площин (рис. 168): пряма, що проходить через ці точки, є спільною для обох площин, т. Е. Їх лінією перетину.
Схему побудови лінії перетину двох площин (див. Рис. 166) можна, звичайно, поширити і на випадок завдання площин їх слідами. Тут роль допоміжних січних площин виконують самі площині проекцій:
Точки перетину однойменних слідів площин є слідами лінії перетину цих площин. Тому для побудови проекцій лінії перетину площин α і β (рис. 168) треба: 1) знайти точку М 'в перетині слідів h'0α і h'0β
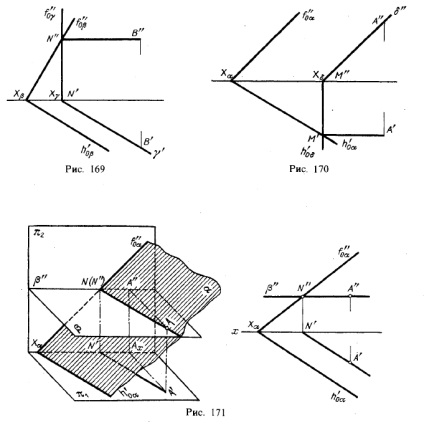
і точку N "в перетині f" 0α і f "0β. а по ним - проекції М" і N '; 2) провести прямі лінії M "N" і M'N ',
На рис. 169-171 показані випадки, коли відомо напрямок лінії перетину. Тому досить мати лйшь одну точку від перетину слідів і далі провести через цю точку пряму, виходячи з положення площин і їх слідів.
Питання до §§ 22-24
- Яке взаємне положення можуть займати дві площини?
- Який ознака паралельності двох площин?
- Як взаємно розташовуються фронтальні сліди двох паралельних між собою фронтально-проектують площин?
- Як взаємно розташовуються горизонтальні сліди двох паралельних між собою горизонтально-проектують площин?
- Як взаємно розташовуються однойменні сліди двох паралельних між собою площин?
- Чи служить ознакою взаємного перетину двох площин перетин хоча б однієї пари їх однойменних слідів?
- Як встановити взаємне розміщення прямої і Площини?
- Як будується точка перетину прямої лінії з площиною, перпендикулярної до однієї або до двох площин проекцій?
- Яка точка з числа розташованих на загальному перпендикуляре до а) пл. π1 б) пл. π2 вважається видимої відповідно на π1. на π2?
- Як будується лінія перетину двох площин, з яких хоча б одна перпендикулярна до пл. π1 або до пл. π2?
- В чому полягає загальний спосіб побудови лінії перетину двох площин?