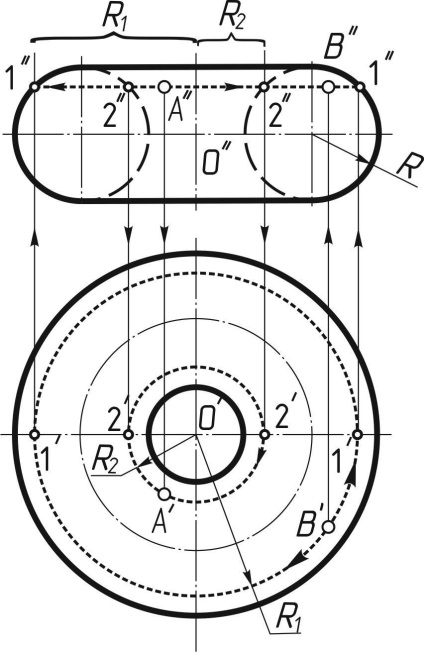
У разі, коли точка А лежить на поверхні кругового кільця і дана одна її проекція, для знаходження другої проекції цієї точки застосовується допоміжна коло, що проходить через дану точку А і розташована на поверхні кільця в площині, перпендикулярній осі кільця (рисунок 145).
Якщо задана фронтальна проекція A '' точки А. лежить на поверхні кільця, то для знаходження її другий проекції (в даному випадку - горизонтальної) через A "проводять фронтальну проекцію допоміжної окружності - відрізок горизонтальної прямої лінії 2''2 ''. Потім будують горизонтальну проекцію 2'2 'цієї окружності і на ній, застосовуючи лінію зв'язку, знаходять точку A '.
Якщо задана горизонтальна проекція B 'точки B. розташованої на поверхні цього кільця, то для знаходження фронтальної проекції цієї точки через 1 'проводять горизонтальну проекцію допоміжної окружності радіуса R1. Потім через ліву і праву точки 1 'и1' цієї окружності проводять вертикальні лінії зв'язку до перетину з фронтальними проекціями нарисової утворює кола радіуса R і отримують точки 1 '' і 1 ''. Ці точки з'єднують горизонтальної прямої, яка представляє собою фронтальну проекцію допоміжної окружності (вона буде видима). Проводячи вертикальну лінію зв'язку з точки B 'до перетину з прямою 1''1' 'отримуємо шукану точку B' '.
Такі ж прийоми побудови можна застосувати й для точок, що знаходяться на поверхні тора.
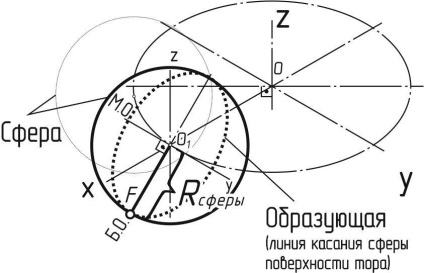
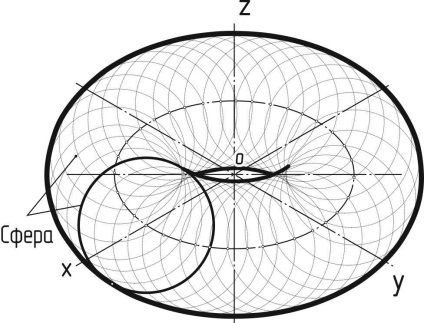
Побудова аксонометричного зображення тора можна розділить на три етапи (рисунок 146). Спочатку будується в вигляді еліпса проекція радіальної осьової лінії (траєкторія руху центру утворює окружності). Потім визначаємо радіус сфери, що стосується тора по котра утворює (кола). Для цього будуємо у вигляді меншого еліпса проекцію фронтальної нарисової утворює тора. Радіус сфери визначимо як довжину відрізка О1 F від центру еліпса до точки на цьому еліпсі, що лежить на великий осі еліпса (перпендикулярній Oy). Далі будуємо велику кількість кіл радіусом Rсфери з центрами на проекції радіальної осьової тора О1 ... Оn (чим більше, тим точніше контур майбутнього тора). На завершення проводимо лінію контуру тора як лінію, що стосується кожного кола сфери.
У аксонометрической проекції точку А. що знаходиться на поверхні тора, будують за трьома координатами: Xа, yа іZА. Ці координати послідовно відкладають по напрямках, паралельним изометрическим осях.