Похідна і диференціал поняття похідної

Попередня ↔ Наступна

Геометричний зміст похідної 1

Фізичний і економічний зміст похідної 2

Диференційовність функції 3

Схема обчислення похідної 5

Основні правила диференціювання 5

Похідні основних елементарних функцій 6

Похідні вищих порядків 7

Еластичність функції 8

Основні теореми про диференціюються функції та їх застосування 9

Екстремуми функції 13

Опуклість функції 16

Асимптоти графіка функції 19

Диференціал функції 22

Застосування диференціала в наближених обчисленнях 24

Поняття про диференціалах вищих порядків 25

Нехай функція у = f (x) визначена на промежуткеX. Візьмемо точку хХ. Дамо значенням х пріращеніех0, тоді функція отримає пріращеніеу = f (x + х) -f (x).

Похідної функції у = f (x) називається границя відношення приросту функції до приросту аргументу при прагненні останнього до нуля (якщо ця межа існує) :.

Похідну також позначають y 'іdy / dx.

Геометричний зміст похідної

Щоб зрозуміти геометричний зміст похідної, розглянемо задачу про дотичній.

Розглянемо на площині графік неперервної функції у = f (x) (див. Рисунок 3.1).

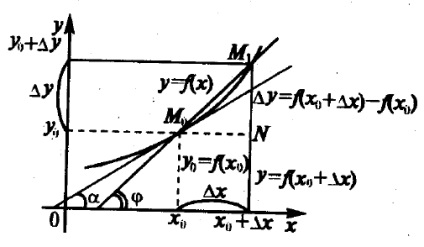
Побудуємо дотичну до цієї кривої в точці М0 (х0. У0). Перш за все, необхідно визначити поняття дотичній. Для цього дамо аргументу х0 пріращеніех і перейдемо на кривій у = f (x) від точки М0 (х0, f (x0)) до точки М1 (х0 + х, f (х0 + х)). Проведемо січну М0 М1. Подкасательной до кривої у = f (x) розуміють граничне положення січної М0 М1 при наближенні точки М1 до точки М0. тобто пріх0.

Кутовий коефіцієнт січної М0 М1 (тангенс угланаклона цієї прямої до осі абсцис) може бути знайдений ізМ0 М1 N:

. Тоді кутовий коефіцієнт дотичній (тангенс угла) дорівнює

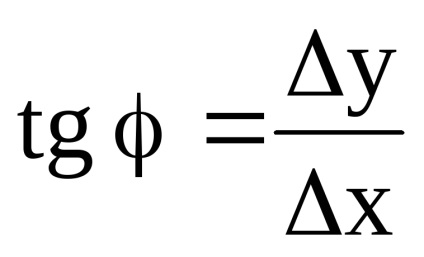
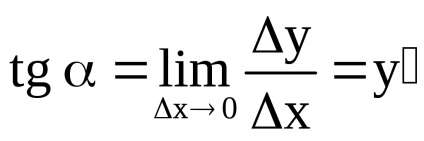
Таким чином, похідна функції являє собою тангенс кута нахилу дотичної до графіка функції до осі абсцис (кутовий коефіцієнт дотичній).

Фізичний і економічний зміст похідної

Розглянемо прямолінійний рух по закону s = s (t), гдеs- пройдений шлях, аt- час. Необхідно знайти швидкість двіженіяvв моментt0.

За проміжок часу tс моментаt0 буде пройдено расстояніеs = s (t0 + t) -s (t0). Тоді середня швидкість за цей проміжок часу составітs / t. Чим менше буде промежутокt, тим краще це відношення буде оцінювати швидкість в момент временіt0:

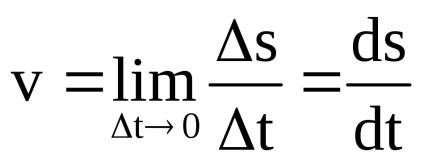
Таким чином, похідна функції являє собою швидкість зміни значення функції в точці. Цей зміст похідної зручно використовувати не тільки у фізиці, але і в економіці.

Наприклад, якщо функція p = p (q) висловлює залежність прібиліpот обсягу виробленої продукцііq, то її похідна показує граничний зростання прибутку (швидкість зміни прибутку при зміні обсягу виробництва):

. Якщо функціяq = q (u) висловлює залежність обсягу проізводстваqот числа работніковu, то її похідна показує швидкість зміни цього обсягу при зміні числа працівників:

(Гранична продуктивність додаткового працівника). Якщо функція описує залежність обсягу виробництва від часу, то отримаємо продуктивність в одиницю часу. Якщо функціяw = w (q) висловлює залежність витрат виробництва від кількості продукції, що випускається, то її похідна означає граничні витрати (приблизно показує додаткові витрати на виробництво одиниці додаткової продукції):

І т.п.

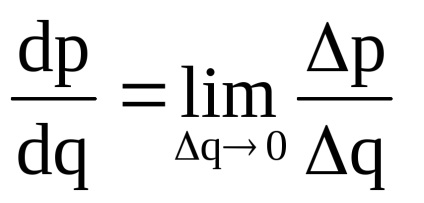
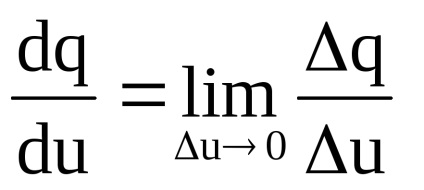
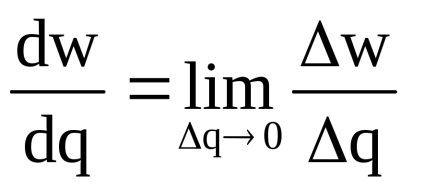
На основі поняття похідної в економіці розраховуються гранична виручка, граничний доход, граничний продукт, гранична корисність, гранична продуктивність та інші граничні величини.

Граничні величини характеризують процес зміни економічного об'єкта. Таким чином, похідна виступає як швидкість зміни деякого економічного об'єкта (процесу) в часі або відносного іншого досліджуваного фактора.

Похідна і диференціал поняття похідної

Геометричний зміст похідної

Фізичний і економічний зміст похідної

Схожі статті