При практичному використанні тих чи інших вимірі важливо оцінити їх точність. Термін «точність вимірювань», т. Е. Ступінь наближення результатів вимірювання до деякого дійсного значення, не має строгого визначення і використовується для якісного порівняння вимірювальних операцій. Для кількісної оцінки застосовується поняття «похибка вимірювань» (чим менше похибка, тим вище точність).
Похибкою називають відхилення результату вимірювань від дійсного (істинного) значення вимірюваної величи-ни. При цьому слід мати на увазі, що справжнє значення фізичної величини вважається невідомим і застосовується в теоретичних дослідженнях. Справжнє значення фізичної величини встановлюється експериментальним шляхом в припущенні, що результат експерименту (вимірювання) в максимальному ступені наближається до істинного значення. Оцінка похибки вимірювання - одне з важливих заходів щодо забезпечення єдності вимірі.
Похибки вимірювань наводяться зазвичай в технічній документації на засоби вимірювань або в нормативних документах. Правда, якщо врахувати, що похибка залежить ще і від умов, в яких проводиться саме вимірювання, від експериментальної помилки методики і суб'єктивних особливостей людини у випадках, де він бере безпосередню участь у вимірюваннях, то можна говорити про декілька складових похибки вимірювань, або про сумарної похибки .
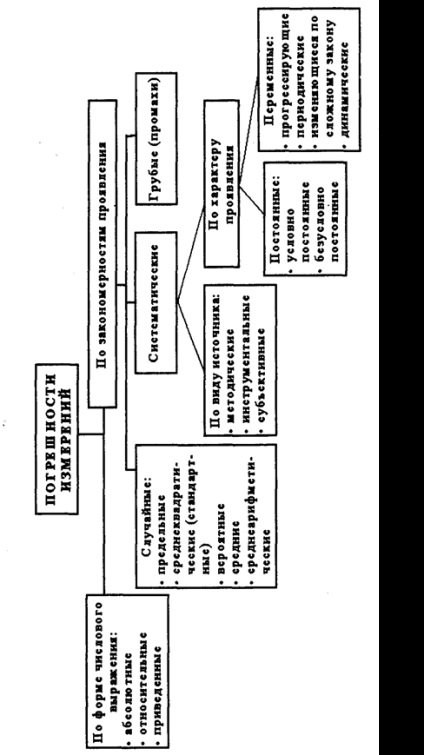
Кількість чинників, що впливають на точність вимірювання, досить велике, і будь-яка класифікація похибок вимірювання (рис.2) певною мірою умовна, так як різні похибки в залежності від умов вимірювального процесу проявляються в різних групах.
2.2 Види похибок
Похибка вимірювання - це відхилення результату вимірювання Х від істинного Хі значення вимірюваної величини. При визначенні похибок вимірювання замість істинного значення фізичної величини Хі. реально використовують її дійсне значення ХД.
Залежно від форми вираження розрізняють абсолютну, відносну і приведену похибки вимірювання.
Абсолютна похибка визначається як різниця # 916; '= Х - ХІ або # 916; = Х - ХД. а відносна - як відношення # 948; = ± # 916; / ХД # 903; 100%.
наведена похибка # 947; = ± # 916; / # 935; # 925; # 903; 100%, де # 935; N - нормирующее значення величини, в якості якого використовують діапазон вимірювань приладу, верхня межа вимірювань і т.д.
Як даного істинного значення при багаторазових вимірах параметра виступає середнє арифметичне значення:
де Xi - результат i -го виміру, - n число вимірювань.
Величина. отримана в одній серії вимірювань, є випадковим наближенням до Хі. Для оцінки її можливих відхилень від Хі визначають оцінку середнього квадратичного відхилення середнього арифметичного:
Для оцінки розсіювання окремих результатів вимірювання Xi щодо середнього арифметичного визначають вибіркове середньоквадратичне відхилення:
Дані формули застосовують при умові постійних через міряють величини в процесі вимірювання.
Ці формули відповідають центральній граничній теоремі теорії ймовірностей, згідно з якою середнє арифметичне з ряду вимірювань завжди має меншу похибку, ніж похибка кожного певного виміру:
Ця формула відображає фундаментальний закон теорії похибок. З нього випливає, що якщо необхідно підвищити точність результату (при виключеної систематичної похибки) в 2 рази, то число вимірів потрібно збільшити в 4 рази; якщо точність потрібно збільшити в 3 рази, то число вимірів
збільшують в 9 разів і т.д.
Потрібно чітко розмежовувати застосування величин S і # 963 ;: перша використовується при оцінці похибок остаточного результату, а друга - при оцінці похибки методу вимірювання. Найбільш ймовірна похибка окремого вимірювання # 916; в 0,67 S.
Залежно від характеру прояву, причин виникнення та можливостей усунення розрізняють систематичну і випадкову похибки вимірювань, а також грубі похибки (промахи).
Систематична похибка залишається постійною або закономірно змінюється при повторних вимірах одного і того ж параметра.
Випадкова похибка змінюється в тих же умовах вимірювання випадковим чином.
Грубі похибки (промахи) виникають через помилкових дій оператора, несправності засобів вимірювання або різких змін умов вимірювань. Як правило, грубі похибки виявляються в результаті обробки результатів вимірювань за допомогою спеціальних критеріїв.
Випадкова та систематична складові похибки через виміри проявляються одночасно, так що їх загальна похибка дорівнює сумі похибок при їх незалежності.
Значення випадкової похибки заздалегідь невідомо, вона виникає через множини не уточнених чинників. Виключити з результатів випадкові похибки не можна, але їх вплив може бути зменшено шляхом обробки результатів вимірювань.
Для практичних цілей досить важливо вміти правильно сформулювати вимоги до точності вимірювань. Наприклад, якщо за допустиму похибку виготовлення прийняти # 916; = 3 # 963 ;, то, підвищуючи вимоги до точності (наприклад, до # 916; = # 963;), при збереженні технології виготовлення збільшуємо ймовірність шлюбу.
Як правило, вважають, що систематичні похибки мо-гут бути виявлені і вилучені. Однак в реальних умовах повністю виключити ці похибки неможливо. Завжди залишаються якісь незвільнені залишки, які потрібно враховувати, щоб оцінити їх межі. Це і буде систематична похибка вимірювання.
Іншими словами, в принципі систематична похибка теж випадкова і вказане поділ обумовлено лише усталеними традиціями обробки і представлення результатів вимірювання.
На відміну від випадкової похибки, виявленої в цілому незалежно від її джерел, систематична похибка розглядається за складовими в залежності від джерел її виникнення. Розрізняють суб'єктивну, методичну та інструментальну складові похибки.
Суб'єктивна складова похибки пов'язана з індивідуальними особливостями оператора. Як правило, ця похибкою-ність виникає через помилки у відліку показань (приблизно 0,1 поділки шкали) і невірних навичок оператора. В основному ж систематична похибка виникає через методичної та інструментальної складових.
Методична складова похибки обумовлена недосконалістю методу вимірювання, прийомами використання засобів вимірювання, некоректністю розрахункових формул і округлення результатів.
Інструментальна складова виникає через власну похибки засобів вимірювання, яка визначається класом точності, впливом засобів вимірювання на результат і обмеженою роздільної здатності засобів вимірювання.
Доцільність поділу систематичної похибки на методичну і інструментальну складові пояснюється наступним:
- для підвищення точності вимірювань можна виділити лімітуючі фактори, а, отже, прийняти рішення про вдосконалення методики або виборі більш точних засобів вимірювання;
- з'являється можливість визначити складову загальної похибки, що збільшується з часом або під впливом зовнішніх факторів, а, отже, цілеспрямовано здійснювати періодичні перевірки і атестації;
- інструментальна складова може бути оцінена до розробки методики, а потенційні точності можливості обраного методу визначить тільки методична складова.
2.3 Показники якості вимірювань
Єдність вимірювань, однак, не може бути забезпечено лише збігом похибок. При проведенні вимірювань також важливо знати показники якості вимірювань. Під якістю вимірювань розуміють сукупність властивостей, що обумовлюють отримання результатів з необхідними точносних характеристиками, в необхідному вигляді та у встановлені терміни.
Якість вимірювань характеризується такими показниками, як точність, правильність і достовірність. Ці показники повинні визначатися за оцінками, до яких пред'являються вимоги спроможності, незсуненості і ефективності.
Істинне значення вимірюваної величини відрізняється від середнього арифметичного значення результатів спостережень на величину систематичної похибки # 916; с. т. е. X = - # 916; с. Якщо систематична складова виключена, то X =.
Однак через обмежений числа спостережень величину точно визначити також неможливо. Можна лише оцінити її значення, вказати з певною ймовірністю межі інтервалу, в якому воно знаходиться. Оцінку числової характеристики закону розподілу Х, зображує точкою на числовій осі, називають точковою. На відміну від числових характеристик оцінки є випадковими величинами, причому їх значення залежить від числа спостережень n. Заможної називають оцінку, яка при n → ∞ зводиться по ймовірності до оцінюваної величиною.
Незміщеної називається оцінка, математичне очікування якої дорівнює оцінюваної величиною.
Ефективною називають таку оцінку, яка має найменшу дисперсію # 963; 2 = min.
Зазначеним вимогам задовольняє середньоарифметичне значення результатів n спостережень.
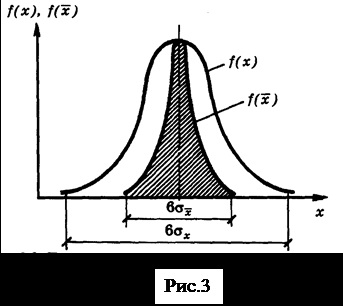
Таким чином, результат окремого вимірювання є випадковою величиною. Тоді точність вимірювань - це близькість результатів вимірювань до істинного значення вимірюваної величини. Якщо систематичні складові похибки виключені, то точність результату вимірювань характеризується ступенем розсіювання його значення, т. Е. Дисперсією. Як показано вище, дисперсія середньоарифметичного # 963; в n разів менше дисперсії окремого результату спостереження.
Достовірність вимірювань визначається ступенем довіри до результату і характеризується ймовірністю того, що істинне значення вимірюваної величини лежить в зазначених околицях дійсного. Ці ймовірності називають довірчими, а кордони (околиці) - довірчими межами. Іншими словами, достовірність вимірювання - це близькість до нуля невиключену систематичної похибки.
Довірчим інтервалом з межами (або довірчими межами) від - # 916; д до + # 916; д називають інтервал значень випадкової похибки, який із заданою довірчою ймовірністю Р д. накриває істинне значення вимірюваної величини.
Рд<- Δд ≤,Х ≤ + Δд>.
При малому числі вимірювань (n 20) і використанні нормального закону не представляється можливим визначити довірчий інтервал, так як нормальний закон розподілу описує поведінку випадкової похибки в принципі при нескінченно великому числі вимірювань.
Тому, при малому числі вимірів використовують розподіл Стьюдента або t - розподіл (запропоноване англійським статистиком Госсетом, публікувалися під псевдонімом «студент»), яке забезпечує можливість визначення довірчих інтервалів при обмеженому числі вимірювань. Межі довірчого інтервалу при цьому визначаються за формулою:
де t - коефіцієнт розподілу Стьюдента, який залежить від заданої довірчої ймовірності Р д і числа вимірювань n.
При збільшенні числа спостережень n розподіл Стьюдента швидко наближається до нормального і збігається з ним вже при n ≥30.
Слід зазначити, що результати вимірювань, що не володіють достовірністю, т. Е. Ступенем впевненості в їх правильності, не уявляють цінності. Наприклад, датчик вимірювальної схеми може мати вельми високі метрологічні характеристики, але вплив похибок від його установки, зовнішніх умов, методів реєстрації та обробки сигналів призведе до великої кінцевої похибки вимірювань.
Поряд з такими показниками, як точність, достовірність і правильність, якість вимірювальних операцій характеризується також сходимостью і відтворюваністю результатів. Ці показники найбільш поширені при оцінці якості випробувань і характеризують їх точність.
Очевидно, що два випробування одного і того ж об'єкта однаковим методом не дають ідентичних результатів. Об'єктивною мірою їх можуть служити статистично обґрунтовані оцінки очікуваної близькості результатів двох або більше випробувань, отриманих при строгому дотриманні їх методики. В якості таких статистичних оцінок узгодженості результатів досл-таний приймаються збіжність і відтворюваність.
Збіжність - це близькість результатів двох випробувань, отриманих одним методом, на ідентичних установках, в одній лабораторії. Відтворюваність відрізняється від збіжності тим, що обидва результати повинні бути отримані в різних лабораторіях.
3. ОТРИМАННЯ І ПОДАННЯ РЕЗУЛЬТАТІВ ВИМІРЮВАННЯ
3.1 Постановка вимірювального експерименту
При постановці вимірювального експерименту, перш за все, потрібно визначити, які за кількістю вимірювань (одноразові або багаторазові) вимірювання слід здійснювати для визначення значення вимірюваної фізичної величини. Загальним тут є наступний підхід:
якщо систематична похибка є визначальною, тобто її значення істотно більше значення випадкової похибки, то доцільно використовувати одноразові вимірювання для отримання значення вимірюваної величини;
якщо випадкова похибка є визначальною, то необхідно використовувати багаторазові вимірювання.
Необхідно враховувати те, що систематична похибка викликає зміщення результатів вимірювань і є найбільш небезпечною тоді, коли про існування її не підозрюють. Виявлення систематичної похибки вимірювань є однією з найбільш складних завдань метрології. У тому чи іншому вигляді її завжди доводиться вирішувати при підготовці до вимірювань.