Очевидно, можуть бути побудовані найпростіші елементи, реалізую-щие елементарні логічні функції двох змінних f0 -f15. Складні логічні функції можуть бути побудовані шляхом послідовного виконання функціональних залежностей, що пов'язують пари змінних.
Отже, маючи елементи, які здійснюють елементарні операції f0 -f15. можна виконати будь-яку складну логічну операцію. Таку систему функцій можна назвати повною системою або базисом. Однак умова наявності 16 різних типів логічних елементів, кожен з яких реалізує одну з 16 елементарних функцій f0 -f15. є умовою, достатнім для синтезу логічного пристрою будь-якої складності, але ця умова не є необхідним, т. е. при синтезі можна обмежитися меншим набором елементарних функцій, узятих з f0 -f15.
Послідовно виключаючи з базису функції, можна отримати так званий мінімальний базис. Під мінімальним базисом розуміють такий набір функцій, виключення з якого будь-який функції перетворює цей набір в неповну систему функцій.
Можуть бути різні базиси і мінімальні базиси, що розрізняються числом що входять в них функцій і видом цих функцій. Вибір того чи іншого базису для синтезу логічного пристрою пов'язаний з тим, наскільки просто, зручно і економічно технічно виконати елементи, що реалізують елементарні функції, які входять в обраний базис, і в цілому все логічний пристрій.
Тепер можна сформулювати умову повноти системи функцій алгебри логіки.
Система функцій буде повною (утворює базис), якщо для будь-якого з п'яти розглянутих властивостей в цій системі знайдеться хоча б одна функція, яка не володіє цією властивістю.
Таким чином, якби повна система була складена з функцій, кожна з яких не володіла хоча б одним з п'яти властивостей, то система включала б у себе п'ять функцій, а шоста була б зайвою. Однак деякі функції не володіють декількома властивостями. Так, наприклад функції «АБО-НЕ», «І-НЕ», не володіють жодним з п'яти властивостей логічних функцій, тому вони утворюють мінімальні базиси і на їх основі можна побудувати логічний вираз будь-якої складності.
Логічне пристрій, реалізоване в базисах «АБО-НЕ», «І-НЕ» має наступні переваги:
-зменшення номенклатури елементів до одного типу спрощує компоновку пристрою і його ремонт;
- наявність в кожному елементі інвертора (підсилювача) компенсує загасання потенціалів при передачі їх через кон'юнктор або діз'юнктор елемента, крім того інвертор збільшує навантажувальну здатність елемента, а наявність ємності на виході не викликає тривалого перехідного процесу при зміні потенціалів.
Саме тому елементи цих базисів широко випускаються промисловістю в інтегральному виконанні.
Розглянемо уявлення логічної функції «Еквівалентність» в базисах «АБО-НЕ», «І-НЕ».
Для конвертування, необхідно логічну функцію двічі проинвертировать і одну інверсію розкрити за правилом Моргана, записуючи логічне вираз через операцію «АБО-НЕ» або «І-НЕ».
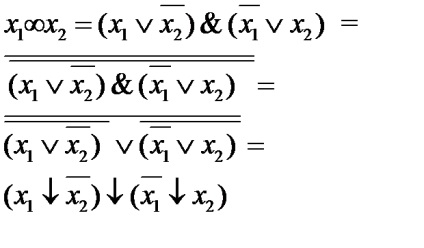
На малюнку 2.1.1 представлена схема, що реалізує операцію «еквівалентність» в базисі «АБО-НЕ».
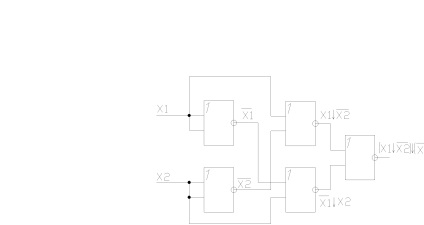
Малюнок 2.1.1. Схема, що реалізує операцію «еквівалентність» в базисі «АБО-НЕ».
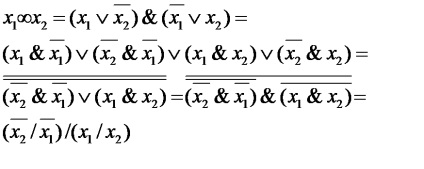
На малюнку 2.1.2 представлена схема, що реалізує операцію «еквівалентність» в базисі «І-НЕ».
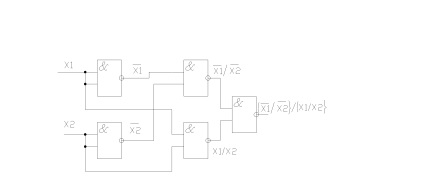
Малюнок 2.1.2. Схема, що реалізує операцію «еквівалентність» в базисі «І-НЕ».