
Головна | Про нас | Зворотній зв'язок
1.4. Визначення внутрішніх зусиль. Метод уявних перетинів
Отже, в опорі матеріалів не враховується реальна атомна структура матеріалу твердого тіла. Виходячи з цього, суцільність і однорідність тіла забезпечується не міжатомними силами, а гіпотетичними внутрішніми зусиллями.
Внутрішні зусилля - сили взаємодії (зчеплення) між частинками тіла, що виникають всередині елемента конструкції, як протидія зовнішньому навантаженню.
Внутрішні зусилля в усіх випадках прагнуть зберегти тіло як єдине ціле, протидіючи будь-якої спробі змінити взаємне розташування частинок, т. Е. Деформувати і зруйнувати тіло. Тому саме величиною внутрішніх зусиль визначається можливість руйнування в тому чи іншому небезпечному перерізі елемента конструкції. Таким чином, для вирішення завдань опору матеріалів необхідно вміти виявляти, а потім визначати величину і напрям внутрішніх зусиль. При їх знаходженні широко використовується метод уявних перетинів.
Виконання гіпотези суцільності твердого тіла, що деформується забезпечується внутрішніми зв'язками ми, природа яких не розглядається в опорі матеріалів. Розрізаючи тіло будь-якої площиною, ми подумки руйнуємо ці зв'язки, але для рівноваги системи замінюємо порушені зв'язки силами, які називаються внутрішніми. Для їх визначення слід розглянути рівновагу будь-якій частині тіла по одну сторону від площини уявного перетину.
Необхідно підкреслити, що з рівнянь рівноваги для залишеної частини тіла визначається не закон розподілу внутрішніх сил, а їх статичний еквівалент в потрібній точці приведення, тобто головний вектор з проекціями N, Qy. Qz і головний момент з проекціями Mx. My. Mz. В опорі матеріалів ці проекції часто називають внутрішніми зусиллями.
Метод уявних перетинів дозволяє відкинути непотрібний для розрахунку елемент конструкції (або частина цього елемента), замінити його силою, дія якої буде еквівалентно дії відкинутого елемента (його частини).
Якщо завдання статично визначна, то для визначення цієї сили досить використовувати рівняння рівноваги (рівняння статики).
Розглянемо який-небудь елемент (наприклад, брус), що знаходиться в рівновазі під дією зовнішніх сил. Нехай потрібно визначити внутрішні зусилля в довільному перерізі бруса.
Застосуємо для цього метод уявних перетинів:
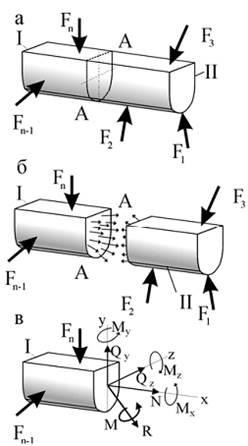
б) відкинемо непотрібну (найбільш складно навантажену) частина елемента, дія відкинутої частини замінимо внутрішніми зусиллями;
в) внутрішні зусилля наведемо до головного вектору R і головного моменту M. головний вектор і головний момент розкладемо по трьох взаємно перпендикулярних осях x, y і z (вісь x - нормальна до перерізу елемента);
г) внутрішні зусилля (N, Qy. Qz. Mx. My. Mz) визначимо з рівнянь рівноваги решти елемента
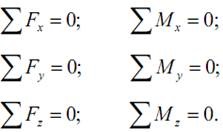
N - осьове (поздовжнє) зусилля. Осьове зусилля дорівнює сумі проекцій на вісь x всіх зовнішніх сил, що діють з одного боку перетину:
Осьове зусилля викликає розтягнення (стиснення) елемента.
Qy. Qz - поперечні сили. Поперечні сили дорівнюють сумі проекцій всіх зовнішніх сил (з одного боку перетину) на осі y і z відповідно:
Поперечні сили викликають зрушення в перерізі елемента.
Mx - крутний момент (T, Mкр). Крутний момент дорівнює сумі моментів зовнішніх сил (з одного боку перетину) щодо осі x:
Крутний момент викликає кручення елемента.
My. Mz - згинальні моменти. Згинальні моменти дорівнюють сумі моментів зовнішніх сил щодо осей y і z відповідно:
Згинальні моменти викликають вигин елемента.
Таким чином, ввівши поняття внутрішніх зусиль, ми отримали можливість звести все різноманіття зовнішніх навантажень і конфігурацій елементів до 6-ти силовим факторам (N, Qy. Qz. Mx. My. Mz) і уявити навіть найскладніше зовнішній вплив як поєднання 4-х видів навантаження: розтягування, зрушення, крутіння, вигину.
Отже, якщо повна система зовнішніх сил відома, то за методом перетинів, завжди можна визначити всі внутрішні зусилля діють в довільно взятому перетині тіла. Дане положення є основоположним обставиною в механіці твердого тіла, що деформується.
Опору, при яких в поперечному перерізі бруса дей-ствует одне внутрішнє зусилля, умовно називаються простими. При одночасній дії в перерізі бруса двох і більше зусиль опір бруса називається складним.
При виконанні практичних рас-четов, для наочності, як правило, визначаються графіки функ-цій внутрішніх силових факторів щодо координатної осі, спрямованої уздовж поздовжньої осі стрижня. Графіки изме-нения внутрішніх зусиль уздовж поздовжньої осі стрижня називаючи-ються епюрами.
1.5. Поняття про нормальних і дотичних напруженнях
Встановити закон (характер) розподілу внутрішніх зусиль по перерізу елемента методами статики не представляється можливим: складаючи рівняння рівноваги для сил, прикладених до відсіченої частини елемента, можемо знайти лише статичний еквівалент внутрішніх зусиль, що виникають в перерізі. Щоб характеризувати закон розподілу внутрішніх зусиль по перерізу елемента, необхідно ввести для них числову міру. За таку міру приймається напруга.
В опорі матеріалів неявно передбачається, що внутрішні зусилля досить рівномірно розподілені на малій майданчику в околиці будь-якої точки уявного перетину. Тому ставлення головного моменту до величини майданчики прагне до нуля разом з цим майданчиком. В результаті
на даному майданчику dA залишається головний вектор сил dR, ставлення якого
до величини площадки dA при стягуванні останньої в точку, називається повним напряженіемp:
Напруга - є внутрішня сила, віднесена до одиниці площі в даній точці розглянутого перетину (інакше кажучи, інтенсивність внутрішнього зусилля в даній точці перетину).
Розмірність напруги: Н / м 2. тобто Па (МПа, кПа)
У розрахунках зручніше користуватися не повним напряженіемp. а його нормальної # 963; і дотичними # 964; складовими. Розглянемо ці поняття.
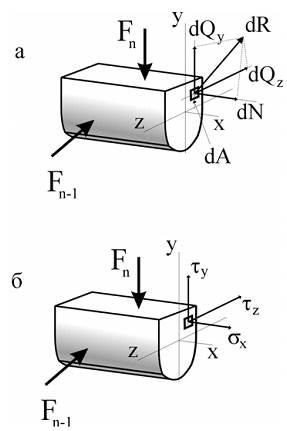
Нормальна напруга (# 963; x) - інтенсивність осьового внутрішнього зусилля, або осьове зусилля, що припадає на одиницю площі в даній точці розглянутого перетину
Дотичне напруження (# 964; y. # 964; z) - інтенсивність внутрішніх поперечних сил, або поперечна сила, яка припадає на одиницю площі в даній точці розглянутого перетину
Таким чином, на майданчику можуть виникати два види напруг: нормальні і дотичні. Відповідно до двома видами напружень на найбільш небезпечною майданчику (там, де напруги максимальні) може реалізовуватися два різних механізму руйнування - відрив або зріз.