Явища інтерференції і дифракції, чітко виявляючи хвильові властивості світла, не відповідають на питання, чи є хвилі поздовжніми або поперечними. Дійсно, зазначені явища спостерігаються для обох типів хвиль будь-якої природи. Зокрема, при однаковій довжині хвилі (наприклад, хвилі довжиною 3 см відповідає акустична частота 10 кГц і оптична, електромагнітна частота 10 10 Гц) явища дифракції можна однаково добре спостерігати на одних і тих же об'єктах. Електромагнітна теорія світла Максвелла пророкує поперечності світлових хвиль. Група явищ, які доводять справедливість передбачення Максвелла, називається явищами поляризації світла. На радіочастотах легко виявити поперечності випромінюваних хвиль і їх лінійну поляризацію: якщо хвиля поширюється вільно, то електричний вектор зберігає в просторі незмінне напрямок; зрозуміло, той же 'справедливо і для магнітного вектора, перпендикулярного електричному. Так, якщо випромінювання здійснюється прямолінійним дротом, а прийомний провід паралельний передавальному, то прийом найбільш сильний; при обертанні приймального дроти навколо прямої, що з'єднує його з передавальним проводом, прийом слабшає і повністю зникає, коли дроти розташовуються взаємно перпендикулярно. З малюнка 7.1 видно, що проекція вектора напруженості (що збігається з напрямком передавального дроти) на напрямок приймального дроти РР становить
Так як ця проекція визначить струм в приймальному пристрої, а інтенсивність прийому пропорційна квадрату струму, то звідси виходить:
Це співвідношення в оптиці носить назву закону Малюса.
Площина, що містить вектор і напрям поширюється від передавача променя, прийнято називати площиною коливань. Площина ж, що містить вектор магнітної індукції хвилі і промінь, називають площиною поляризації. Очевидно, ці площини взаємно перпендикулярні.
Такий же закон зміни інтенсивності проходить хвилі виходить, якщо між паралельними випромінювачем і приймачем помістити грати з паралельних металевих дротів (в площині, нормальної вектору швидкості хвилі) і обертати її у власній площині. Чи не пропущена гратами енергія хвилі відбивається від решітки; невеликим поглинанням в металі можна знехтувати.
Зрозуміло, при поздовжніх коливаннях ніякої поляризації бути не може, так як всі площини, що проходять через промінь, рівноправні.
Для кращого розуміння дослідів, що виявляють поперечності світлових хвиль, розглянемо попередньо кілька дослідів з сантиметровими електромагнітними хвилями.
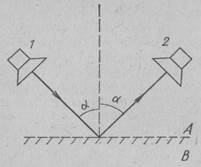
Генератор оснащений рупором, що створює лінійну (плоску) поляризацію випромінюваних хвиль. Вектор електричного поля лежить паралельно вузькій стороні рупора, що можна перевірити на досвіді, приймаючи хвилю прямолінійним провідником. Розташуємо передає рупор 1 так, щоб коливання вектора відбувалися в площині малюнка (рис. 7.2). Приймальний рупор 2 маємо так, щоб він міг приймати випромінювання, що відображається деяким перешкодою, якщо вектор хвилі, що приходить лежить в плоскостірісунка. Це перешкода являє собою набір паралельних дротів, розташованих в площинах, паралельних кресленням, і здатних повертатися в цих площинах. При положенні А всякому кутку падіння можна підібрати рівний кут відображення а, і приймач завжди відзначить прийом, хоча і різною (для різних кутів падіння) інтенсивності.
Але якщо розташувати дроту решітки в напрямку відбитого променя (положення В), то прийом припиняється. Причина цього зрозуміла: так як порушені дроту можна уподібнити диполя (див. «Електрика і магнетизм», § 12.4), а диполі не випромінюють в напрямі своєї осі, то, коли ця вісь збігається з напрямком відображення, визначеним принципом Гюйгенса, відбитий промінь утворитися не може.
Якщо ж повернути обидва рупора на 90 ° навколо їх осей, щоб вектор став перпендикулярний площині креслення (а це є площину падіння!), То відображення від дротів, які тепер слід також вивести з площини креслення, існує завжди (звичайно, в напрямку відбитого променя , т. е. під кутом α). І цей результат зрозумілий: тепер вісь диполя ніколи не збігається з напрямком відбитого променя, а тому відображення завжди існує.
Отже, якщо електричний вектор падаючого променя лежить в площині падіння, то можна домогтися зникнення відбитого променя. Якщо ж він перпендикулярний цій площині, то відображення знищити неможливо.