Глава 4. Математичні моделі оптимізації
1. Функцію f (x) називають опуклою, якщо вона цілком лежить не вище відрізка, що з'єднує дві її довільні точки. Функцію називають строго опуклою, якщо вона цілком лежить нижче відрізка, що з'єднує дві її довільні, але не збігаються точки.
2. Якщо функція сильно опукла, то вона одночасно строго опукла і опукла. Якщо функція строго опукла, то вона одночасно опукла.
3. Опуклість функції можна визначити по матриці Гессе:
· Якщо H (x) ³ 0 "x Î R n. то функція опукла;
· Якщо H (x)> 0 "x Î R n. то функція строго опукла;
· Якщо H (x) ³ lE "x Î R n. де Е - одинична матриця, то функція сильно опукла.
Відзначимо важливу властивість опуклою функції. Якщо функція f опукла на безлічі X, то для будь-яких точок x1. x2. xm ÎX і довільних невід'ємних чисел l1 + l2 +. lm = 1 має місце нерівність Ієн Сена
При m = 2 ця нерівність збігається з нерівністю (3.1) з визначення опуклої функції.
Сама по собі постановка задачі оптимізації проста і природна: задані безліч Х і функція | (x), певна на х, потрібно знайти точки мінімуму або максимуму функції | на х. Завдання на мінімум запишемо у вигляді:
При цьому | будемо називати цільової функцією. х - допустимим безліччю, будь-який елемент х ÎХ - допустимої точкою завдання (4.1). Якщо х збігається з усім простором, завдання 4.1 називається завданням безумовної мінімізації (без обмежень), в іншому випадку - задачейусловной мінімізації (з обмеженнями).
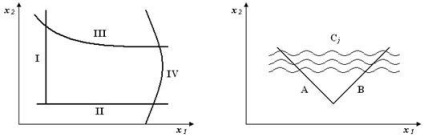
а) на лінійні (I, II) і нелінійні (III, IV) (рис.4.1);
б) детерменірованние (А. В) і стахостатіческіе (групи кривих Сj) (рис.4.2).
Мал. 4.3 Довільна крива з двома локаль- Рис.4.4 Одномірні унімодальне функції ними і одним глобальним мінімумами.
Таким чином, глобальний мінімум - це найменший з усіх локальних мінімумів. На рис. 4.3 показані точки локальних і глобального мінімумів для довільної кривої | (x).
Завдання оптимізації, в якій критерій оптимальності | (x) має в області Х єдиний локальний мінімум, називається одноекстремальной (унімодальної) завданням оптимізації. Найпростішими з унімодальних функцій є опуклі функції (рис. 4.4.а).
На рис.4.4 наведені приклади унімодальних одновимірних функцій.
Завдання оптимізації, в якій критерій оптимальності | (х) має кілька локальних мінімумів, називається багатоекстремального завданням оптимізації.
Звичайні методи рішень багато екстремальних задач забезпечують знаходження лише окремої особливої точки, в якій приватна похідна. Такою точкою в залежності від випадкових обставин (вибір початкового наближення) може бути будь-який з локальних мінімумів або точка перегину. У зв'язку з цим істотне значення має дослідження умов, при яких рішення забезпечує знаходження глобального мінімуму.
Якщо нерівність в (4.2) або (4.3) виконується як суворе при х¹х *, то кажуть, що х * -точка суворого мінімуму (суворе рішення) в глобальному або локальному сенсі. Ясно, що глобальне рішення є і локальним; зворотне невірно.
Для відображення того факту, що точка х *ÎХ є точкою глобального мінімуму функції | на Х, будемо використовувати запис:
або еквівалентна їй запис
При цьому говорять, що точка х * реалізує величину, тобто. мінімальне значення функції | на Х. Безліч всіх точок глобального мінімуму | на Х позначимо через
Таким чином, Argmin| (x) -це просто довільна точка з безлічі.
При необхідності задачу мінімізації можна замінити завданням максимізації або навпаки. Це пояснюється тим, що мінімум функції | дорівнює максимуму функції -|, взятому з протилежним знаком, і досягаються обидва ці екстремуму при одних і тих же значеннях змінних (рис.4.5). У точці х * min| (x *) = -max (-| (x *)).
Рис.4.5 До постановки задачі оптимізації.
Таким чином, якщо, наприклад, задачу мінімізації функції при будь-яких обмежень потрібно замінити завданням максимізації, то досить замість взяти в якості цільової функцію -, знайти максимум цієї функції і замінити його знак на протилежний. Отримане значення буде оптимумом вихідної задачі. За анологіі з (4.1) будемо записувати завдання максимізації функції | на безлічі Х у вигляді:
Рішення задач (4.1) і (4.4), тобто точки мінімуму і максимуму функції | на Х називають також точками екстремуму. а самі завдання (4.1) і (4.4) -екстремальнимі завданнями.