

Проект представляють студенти автотранспортного коледжу: МалолетневЕвгеній, Новіков Олексій і КостерёвІван. Вивчаючи інформатику, ми помітили, що вона тісно пов'язана з математикою. На заняттях ми дізналися, які відкриття в області математики привели до появи комп'ютерів, без яких ми не уявляємо своє сучасне існування. У своїй роботі ми хотіли познайомити вас з цими відкриттями.


Ми поставили за мету простежити історію виникнення цифр і систем числення. Нам стало цікаво, хто стоїть біля витоків двійковій системи числення, як давно і де її почали застосовувати, чому двійкова система числення збереглася до наших днів.


На ранніх щаблях розвитку суспільства люди майже не вміли рахувати. Велике число предметів вони об'єднували в понятті «багато». Це був ще не рахунок, а лише його зародок.
Особливо важливу роль грав природний інструмент людини - його пальці. Цей інструмент не міг довго зберігати результат рахунку, але зате завжди був «під рукою».


Поняття «число» є ключовим як для математики, так і для інформатики. Люди здавна вважали і записували числа. Але записували їх за різними правилами. Число зображувалося за допомогою одного або декількох символів, які називалися цифрами.


У найдавніші часи числа позначалися прямолінійними позначками ( «паличками»); одна паличка зображувала одиницю, дві палички - двійку. Цей спосіб походить від зарубок для запису минулих днів.
Перші написані цифри, про які ми маємо достовірні свідчення, з'явилися в Єгипті і Месопотамії близько п'яти тисяч років тому.


Від пальцевого рахунку бере початок п'ятіркова система числення (одна рука), десятеричная (дві руки), двадцатерічная (пальці рук і ніг).
Пізніше з'явилося поняття системи числення. Системою числення називають систему правил, що дозволяють встановлювати
відповідність між будь-яким числом і його поданням. Безліч символів, використовуваних для такого уявлення, називають цифрами.


У давнину багато народів не спілкувалися один з одним, тому в різних народів виникли різні системи числення. Люди прийшли до розумного рішення - записувати числа по розрядах: окремо одиниці, окремо десятки, окремо сотні.
Так з'явилися позиційні системи числення. У позиційній системі числення значення цифри визначається її положенням в числі.


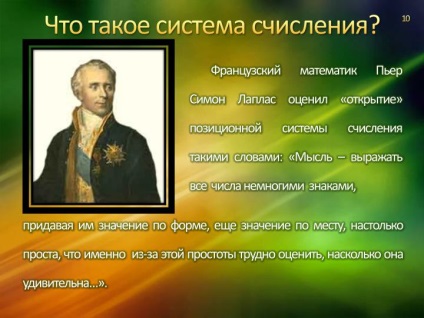
Французький математик П'єр Симон Лаплас оцінив «відкриття» позиційної системи числення такими словами: «Думка - висловлювати все числа небагатьма знаками,
надаючи їм значення за формою, ще значення за місцем, настільки проста, що саме через цю простоту важко оцінити, наскільки вона дивовижна ... ».



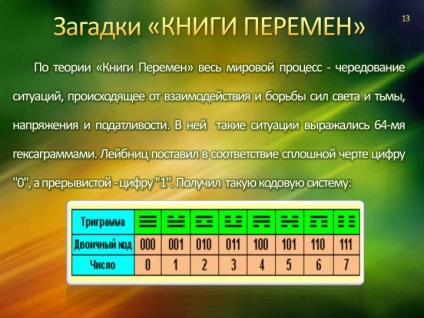
Як людина, що захоплюється китайською культурою, Лейбніц знав про книгу Змін. Лейбніца зацікавили загадкові написи, які не могли пояснити китайські вчені. Написи складалися з ряду довгих і коротких рисок. З найдавніших часів і до наших днів «Книга Змін» мала великий вплив на все життя китайського суспільства.

За теорією «Книги Змін» весь світовий процес - чергування ситуацій, що походить від взаємодії і боротьби сил світла й темряви, напруги і податливості. У ній такі ситуації виражалися 64-ма гексаграммами. Лейбніц поставив у відповідність суцільний межах цифру "0", а переривчастої - цифру "1". Отримав таку кодову систему:

Описуючи двійкову систему, Лейбніц з'ясував, що існують цілком нові закони математики. Він відзначав особливу простоту алгоритмів дій в двійковій арифметиці в порівнянні з іншими системами. Правила виконання дій задаються таблицями двійкових додавання, віднімання і множення.


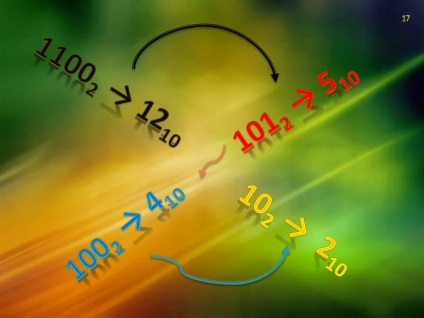
Медаль, намальована Лейбніцем, в 1697 р пояснює співвідношення між двійковій і десяткової системами числення


Їй було 1100 років
Вона в 101 клас ходила
У портфелі по 100 книг носила
Все це правда, а не марення.
Коли пилять десятком ніг,
Вона крокувала по дорозі,
За нею завжди біг щеня
З одним хвостом, зате 100 - ногій
Вона ловила кожен звук
Своїми 10-ю вухами
І 10 засмаглих рук портфель і поводок тримали
І 10 темно-синіх очей оглядали світ звично
Але чи стане все зовсім звичайним,
Коли зрозумієте наша розповідь.



Точка і тире виявилися самими елементарними символами, які міг передавати телеграф Морзе. Вони відповідали коротким і довгим імпульсам електричного струму, що передаються по телеграфним проводам. Азбука Морзе ставить у відповідність кожній букві алфавіту послідовність з крапок і тире.






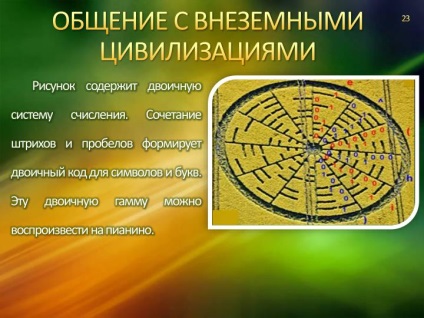
Піктограма в Чілболтоне стала відповіддю на наше земне послання. Складна піктограма, представляє таблицю двійкового коду. За структурою вона повторювала радіопослання землян.




Малюнок містить двійкову систему числення. Поєднання штрихів і прогалин формує двійковий код для символів і букв. Цю двійкову гаму можна відтворити на піаніно.

Паперові носії були наіболееудобним способом введення інформації. Перші перфокарти використовувалися в ткацьких верстатах Жаккарда. Цифра кодується одним отвором, буква -
двома отворами. У счетнихмашінах вони використовувалися до 1980-го року.

У супермаркетах на упаковках товарів можна побачити штрих-код. Він потрібен для занесення інформації в касовий апарат. Сканер сприймає кожну чорну смужку як послідовність одиниць довжини від однієї до чотирьох, проміжки між полосамі- як нулі. Товщина смуг може приймати чотири значення - від найтоншої до самої товстої.

Таблицю двійкових чисел легко перетворити в набір карт для вгадування мислей.Каждому десятковому числу відповідає двійковий код.
Можна зробити п'ять карт з числами, де кожен стовпець чисел випісиваетсяна окремій картці.

Треба дати людині картки і попросити задумати будь-яке число від 0 до 31. Попросіть повернути ті картки, на яких зустрічається це число.
Отримавши картки, ви відразу ж можете назвати задумане число.


Студент загадав число 13. Він повернув три картках з п'яти, з цим числом. У кожній картці счітаемпервий цифри, унас вони - 4, 8, 1. Їх підсумовуємо і отримуємо відгадку: 4 + 8 + 1 = 13. І так вийшло число 13 яке загадав студент. Досвід пройшов успішно.
Кожне задумане число задає особливу комбінацію.

Проект обчислювальної машини, що працює в двійковій системі, Лейбніц виклав у праці, написаному в 1679 році. Він намагався застосувати двійкового коду в механіці і зробив креслення обчислювальної машини, яка працювала на основі його нової математики. Але незабаром зрозумів, що технологічні можливості його часу не дозволяють створити таку машину.

Особливу роль в історії цивілізації відіграє винахід електронних обчислювальних машин, які ми називаємо комп'ютерами. Перші ЕОМ грунтувалися на десятковій системі числення, але пізніше згадали про двійкову систему.
У чому ж перевага цієї системи числення?

- Перші виконавчі ЕОМ були побудовані на принципах, викладених Джоном фон Нейманом. В обчислювальних машинах коди нуля і одиниці видаються електрично-ми сигналами, в двох станах.

Математичний апарат алгебри логіки виявився дуже зручний для опису того, як функціонують апаратні засоби комп'ютера. Основною системою числення в комп'ютері є двійкова, в якій використовуються цифри 1 і 0, а значень логічних змінних теж два:
"1" і "0". Творець алгебри Логіки - Джон Буль. За допомогою алгебри Буля можна просто скласти схему автомата, що працює на реле.

Однією з найбільш досконалих релейних обчислювальних машин була машина РВМ-1, сконструйована і побудована під керівництвом радянського інженера Н.І.Бессонова в середині 50-х років.

Завдяки застосуванню каскадного принципу виконання арифметичних операцій, винайденого самим Бессоновим, машина виробляла до 1250 умножений в хвилину. Вона містила 5500 реле. Цілий ряд удосконалень настільки поліпшив її надійність і експлуатаційні якості, що вона працювала до 1965 року.

36 перевірили, як вони працюють
Комп'ютерний світ з кожним роком ускладнюється. Потужність обчислювальної техніки подвоюється кожні півтора року. Персональні комп'ютери, на яких сьогодні грають школярі, могутніше суперкомп'ютерів недавнього минулого. Випускаються все більш продуктивні операційні системи, з'являються зовсім нові області застосування комп'ютерів.

Висновок перевірили, як вони працюють

Гутер Р.С. Полунов Ю.Л. - Від абака до комп'ютера (Бібліотека ЗНАННЯ) - +1981
Фомін С.В. Системи числення. М. Наука, 1987.
Решетніков В.Н. Сотников О.М. Інформатика - що це? М. Радио и связь, 1989.
