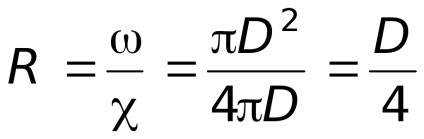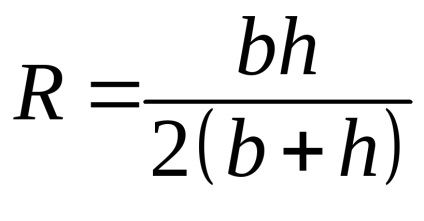На основі рівняння Бернуллі сконструйований ряд приладів, таких, як водомір Вентурі, водоструминний насос, ежектор, карб-ра-тори поршневих двигунів і ін.
Приклад 1. Водомір Вентурі є короткий від-різкий труби зі звуженням посередині (рис. 3.13). У широкої частини і гір-Ловіна встановлюються або п'єзометри, або диференціальних-ний манометр.
Застосуємо рівняння Бернуллі для перетинів 1-1 і 2-2 без обліку втрат і при
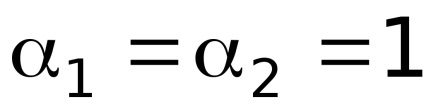

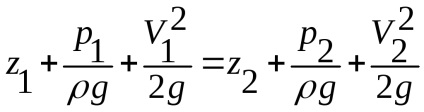
Перетворимо рівняння наступним чином:

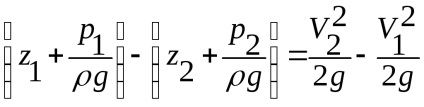
Згідно (рис. 3.13) різниця в лівій частині дорівнює h.
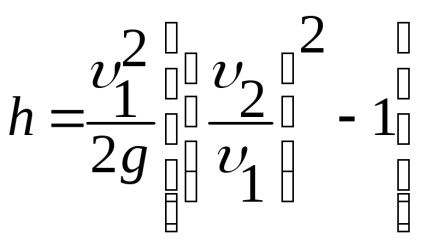
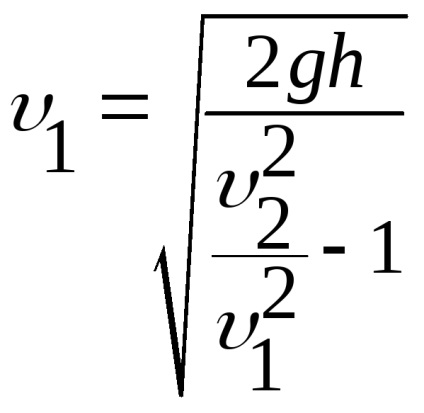
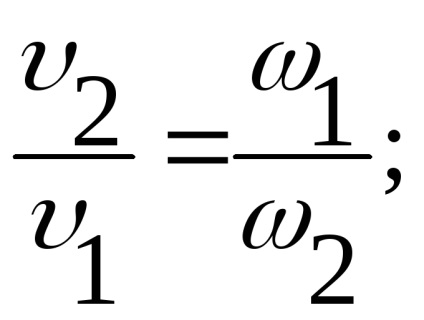
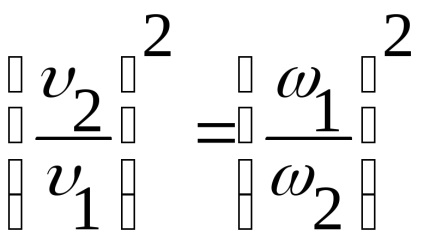

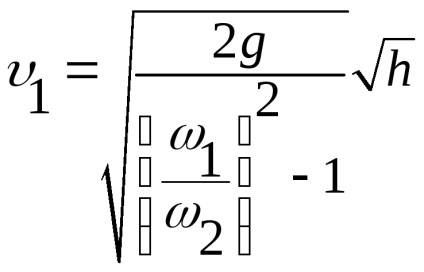
Використовуючи рівняння витрати
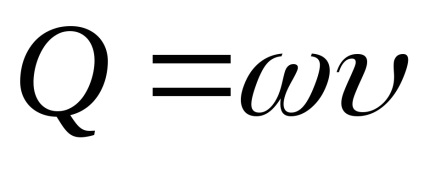
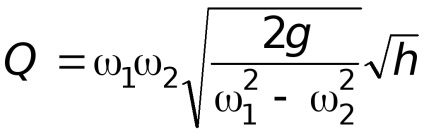
Позначимо постійні величини через
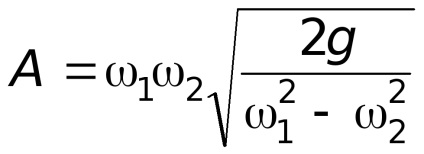
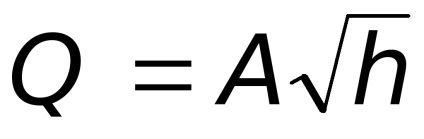
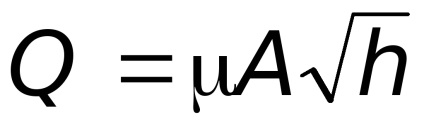
коефіцієнт витрати водоміра.
Приклад 2. Карбюратор поршневих двигунів внутрішнього згор-Ранія служить для здійснення подачі бензину і змішання його з потоком повітря (рис. 3.14). Потік повітря, засмоктуваний в дві-гатель, звужується там, де встановлений розпилювач бензину.
Швидкість повітря в цьому перерізі зростає, а тиск з рівняння Бернуллі падає.
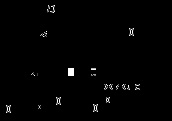
Знайдемо співвідношення між ваговим витратою бензину Gб і воздухаGв при заданих размерахD иd і коефіцієнтах со-про-тив-лення повітряного каналу (до перетину 2-2) в і жіклераж.
Запишемо рівняння Бернуллі для потоку повітря (перетину 0-0 і 2-2), а потім для потоку бензину (перетину 1-1 і 2-2) і отримаємо при
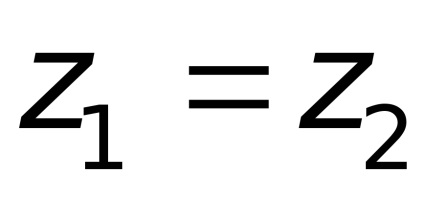
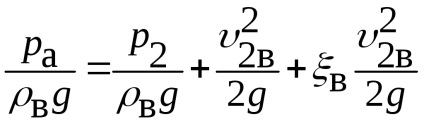
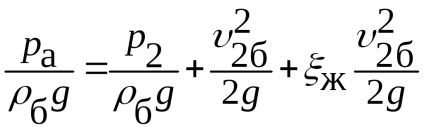
.
З урахуванням вагових витрат
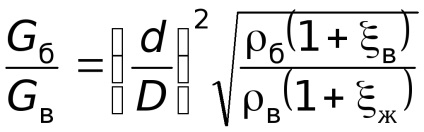
Приклад 3. Трубка Піто широко застосовується для вимірювання швидкості води і газу. Складемо рівняння Бернуллі для перетинів 1-1 і 2-2. Го--різонтального площину порівняння 0-0 проходить через носок трубки (рис. 3.15)
.
Так як
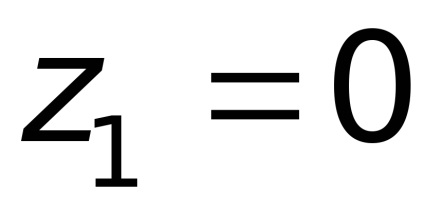
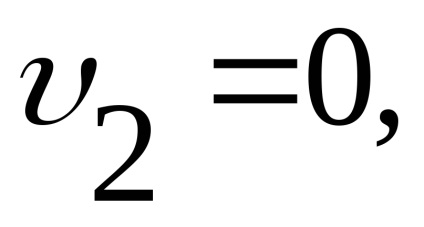
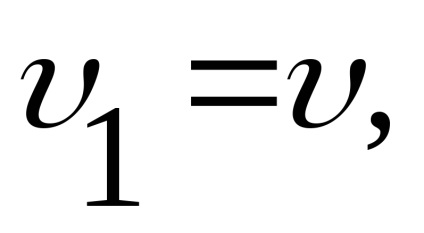

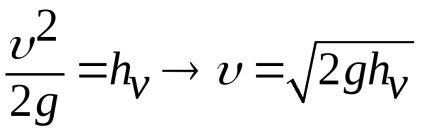
Контрольні питання
1. Напишіть рівняння Бернуллі для елементарної цівки нев'язкої рідини і поясніть величини, що входять в нього.
2. Чим відрізняється рівняння Бернуллі для потоку реальної рідини від рівняння Бернуллі для елементарної цівки?
3. Що називається повною питомою енергією потоку?
4. Поясніть фізичний зміст коефіцієнта Коріоліса в рівнянні Бернуллі.
5. Поясніть енергетичний сенс рівняння Бернуллі.
6. Що називається пьезометрические і гідравлічним ухилами?
7. Наведіть приклади практичного застосування рівняння Бер-Нулла.
8. На основі якої моделі отримано висновок рівняння Бернуллі для потоку реальної жідкості
9. Що таке п'єзометричний і швидкісний натиск?
Що називається повним напором?
3.12. Гідравлічні опору. Режими руху рідини
При русі реальних рідин в різних гідросистемах потрібна точна оцінка втрат напору на подолання гідрав-ли-чеських опорів. Точний облік цих втрат багато в чому оп-ре-деляет надійність технічних розрахунків. Крім того, це дозволяє знайти економічно доцільне інженерне рішення, про-Лада-ний достатнім ступенем досконалості. Для цього необ-ді-мо мати чітке уявлення про механізм руху рідини.
У процесі досліджень відомий фізик Рейнольдс в 1883 го-ду підтвердив теорію про існування двох режимів руху жид-кістки. Це перш за все ламінарний режим руху жид-кістки, відповідний малим швидкостям. Ламінарний рух можна розглядати як рух окремих шарів рідини, що відбувається без перемішування частинок.
При більш високих швидкостях руху рідини спостерігається турбулентний режим ( «турбулентус» по-латині - вихровий). Та-де-не рух називають безладним.
Для оцінки режиму руху рідини Рейнольдс ввів без-розмірний критерій Re, який враховує вплив швидкості

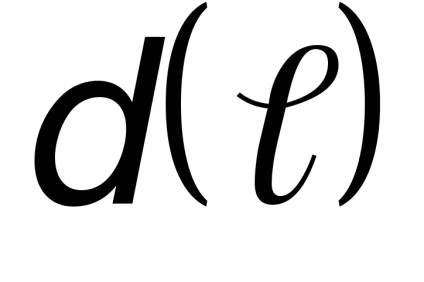
Кордон існування того чи іншого режиму руху жид-кістки визначається двома критичними значеннями числа Re: ниж-ним


Так, при