Приклад 1. Заряди q1 = 3нКл і q2 = -5нКл знаходяться на відстані r = 6см один від одного. Визначити напруженість Е і потенціал # 966; в точці, що знаходиться на відстані a = 3 см від першого заряду і d = 4 см від другого заряду. Якою силою потрібно утримати в цій точці заряд q 3 = 1нКл?
Рішення . Згідно з принципом суперпозиції електричних полів, кожен заряд створює поле незалежно від присутності в просторі інших зарядів. Тому напруженість електричного поля в шуканої точці може бути знайдена як геометрична сума напруженостей і полів, створюваних кожним зарядом окремо:.
Напруженість електричного поля, створюваного в повітрі (# 949; = 1) зарядом q1. дорівнює
Вектор спрямований по силової лінії від заряду, так як заряд q1 позитивний; вектор спрямований також по силової лінії, але до заряду q2. так як заряд q2 негативний.
Абсолютне значення вектора Е найдти по теоремі косинусів:
В даному випадку, щоб уникнути громіздких записів зручно значення cos # 945; обчислити окремо:
Підставляючи вирази і в і виносячи загальний множник за знак кореня, можна отримати:
Силу F. яка буде потрібно, щоб утримати заряд в точці В, знаходять за формулою
Потенціал j результуючого поля, створюваного двома зарядами q1 і q2. дорівнює сумі алгебри потенціалів, тобто
Потенціал електричного поля, створюваного в вакуумі точковим зарядом q на відстані r від нього, виражається формулою
В даному випадку виразиться як:
Приклад 2. Пластини плоского конденсатора, заряджені зарядом q = 15нКл. притягуються в повітрі з силою F = 600мкН. Визначити площу пластин конденсатора.
Рішення . Заряд q однієї пластини знаходиться в полі напруженістю Е1. створеному зарядом одної пластини конденсатора. Отже, на перший заряд діє сила
де # 963; - поверхнева щільність заряду пластини, то
Приклад 3. Заряд величиною 1 нКл переноситься з нескінченності в точку, що знаходиться на відстані 0,1 м від поверхні металевої сфери радіусом 0,1 м, зарядженої з поверхневою щільністю. Визначити роботу переміщення заряду
Рішення . Потенціал поля. створюваного зарядженої сферою на відстані від її центру, визначається за формулою:
де заряд сфери; електрична постійна.
Потенціал поля на відстані дорівнює нулю:. Робота А по переміщенню заряду q з нескінченності в точку поля дорівнює:
Приклад 4. Енергія плоского повітряного конденсатора 40 нДж, різниця потенціалів на обкладках 600 В, площа пластин 1 см 2. Визначити відстань між обкладинками, напруженість і об'ємну щільність енергії поля конденсатора.
Рішення . Енергія конденсатора; ємність конденсатора. отже,. Звідси
Напруженість поля конденсатора
Густина енергії поля:
Приклад 5. Електрон, що володіє кінетичної енергією Т1 = 10еВ, влетів в однорідне електричне поле з напруженістю Е = 10В / м в напрямку поля і пройшов в ньому відстань r = 50 см. Визначити швидкість електрона в кінці зазначеного шляху.
Рішення . Відповідно до визначення вектора напруженості електричного поля. на електрон, що влетів в напрямку вектора напруженості поля, діє сила. спрямована протилежно руху. Следо-вательно, електрон гальмується під дією цієї сили. На шляху руху електрона електричне поле здійснює роботу А.
де е - заряд електрона; е = 1,6 # Тисяча шістсот тридцять два; 10 -19 Кл.U - різниця потенціалів на шляху руху.
Робота сил електричного поля, витрачена на зміну кінетичної енергії електрона
де Т1. Т2 - кінетичні енергії електрона до і після проходження уповільнює поля.
Кінетична енергія електрона в кінці шляху
З огляду на однорідність електричного поля можна написати, що:
Скориставшись зазначеними формулами, можна отримати:
Тоді швидкість електрона в кінці шляху
Приклад 6. На кінцях мідного дроту довжиною l = 5м підтримується напруга U = 1В. Визначити щільність струму j в проводі.
Рішення . Згідно із законом Ома в диференціальній формі
питома провідність # 947; визначається як
де # 961; - питомий опір міді
Напруженість електричного поля всередині провідника відповідно до формули, що зв'язує різниця потенціалів (напруга) і напруженість в однорідному електричному полі виражається формулою
Використовуючи вищевказані формули:
Приклад 7. Визначити електричний заряд, що пройшов через поперечний переріз проводу опором R = 3Ом при рівномірному наростанні напруги на кінцях дроти від U1 = 2В до U2 = 4В протягом # 916; t = 20с.
Рішення . Відповідно до закону Ома змінну напругу викликає в провіднику змінний струм. За визначенням сили струму
де dq - кількість електричного заряду, що пройшов через поперечний переріз провідника за нескінченно малий проміжок часу dt. I - миттєве значення сили змінного струму.
де U - миттєве значення напруги.
При рівномірному наростанні напруги його миттєве значення в момент часу t одно
де k - швидкість наростання напруги, що дорівнює приросту напруги за одиницю часу. При рівномірному наростанні
Використовуючи вищевказані формули, можна обчислити
Приклад 8. Сила струму в провіднику опором R = 20ом наростає протягом часу # 916; t = 2 с за лінійним законом від I0 = 0 до I = 6А. Визначити теплоту Q1. виділилася в цьому провіднику за першу і Q2 - за другу секунди, а також визначити ставлення.
Рішення . Згідно із законом Джоуля-Ленца
Тут сила струму є деякою функцією часу:
де k - коефіцієнт пропорційності, чисельно рівний збільшенню сили струму в одиницю часу. При лінійному законі
При визначенні теплоти, що виділилася за першу секунду, межі інтегрірованіяt1 = 0. t2 = 1 c і, отже,
тобто за другу секунду виділиться теплоти в 7 разів більше, ніж за першу.
Приклад 9. По дроту, зігнутому у вигляді квадрата зі стороною a = 10 см тече струм силою I = 100A. Знайти магнітну індукцію в точці перетину діагоналей квадрата.
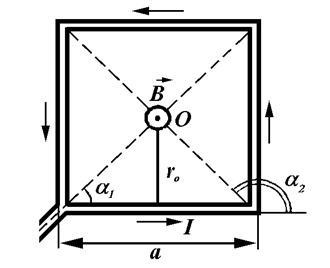
Рішення. Квадратний виток розташований в площині креслення.
Згідно з принципом суперпозиції магнітних полів магнітна індукція поля квадратного витка буде дорівнює геометричній сумі магнітних індукцій полів, створюваних кожною стороною квадрата окремо:
У точці Про перетину діагоналей квадрата всі вектори індукції для зазначеного на рис. струму будуть спрямовані перпен-дікулярно площині витка «до нас». Крім того, з міркувань симетрії випливає, що читається ну ніяк значення цих векторів однакові:. Це дозволяє векторне рівність замінити скалярним рівністю
Магнітна індукція В1 поля, створюваного відрізком прямолінійного проводу зі струмом, виражається формулою
З огляду на, що і. формулу можна переписати у вигляді
Тут і (так як), і тоді В.
Підставивши в цю формулу числові значення фізичних величин, для В вийде значення:
Приклад 10. Електрон, пройшовши прискорює різниця потенціалів U = 400В. потрапив в однорідне магнітне поле напруженістю H = 10 3 А / м. Визначити радіус R кривизни траєкторії і частоту n обертання електрона в магнітному полі. Вектор швидкості перпендикулярний лініям поля.
Рішення . Радіус кривизни траєкторії електрона можна визначити, виходячи з таких міркувань: на рухомий в магнітному полі, діє сила Лоренца (дією сили тяжіння можна знехтувати). Сила Лоренца перпендикулярна вектору швидкості і, отже, повідомляє електрону нормальне прискорення:
R - радіус кривизни траєкторії, # 945; - кут між напрямком вектора швидкості і вектором (в даному випадку і # 945; = 90 °. sin # 945; = 1)
Тоді для R знаходиться формула:
Вхідний в цю рівність імпульс m # 965; може бути виражений через кінетичну енергію Т електрона:
Але кінетична енергія електрона, що пройшов прискорює різниця потенціалів U. визначається рівністю
Підставивши цей вираз Т в вираз для вийде вираз:
Магнітна індукція В може бути виражена через напруженість Н магнітного поля в вакуумі
Використовуючи отримані вирази можна визначити R у вигляді:
Для визначення частоти звернення n можна скористатися формулою, що зв'язує частоту зі швидкістю і радіусом:
З урахуванням вийде:
Приклад 11. В однорідному магнітному полі (В = 0,1 Тл) рівномірно з частотою n = 10об / с обертається рамка, яка містить N = 1000 витків, які щільно прилягають одна до одної. Площа рамки S = 150см 2. Визначити миттєве значення е.р.с. індукції. відповідне куту повороту рамки 30 °.
Рішення . Миттєве значення е.р.с. індукції визначається основним рівнянням електромагнітної індукції
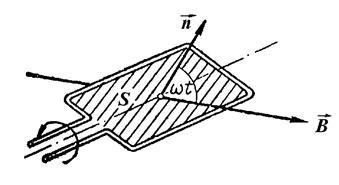
При обертанні рамки магнітний потік Ф. пронизливий рамку в момент часу t. змінюється за законом
де В - магнітна індукція,
# 969; - кругова (циклічна) частота.
Продифференцировав за часом Ф, можна знайти миттєве значення е.р.с. індукції у вигляді:
З огляду на, що частота # 969; пов'язана з частотою обертання n співвідношенням
Приклад 12. Соленоїд без сердечника має щільну одношарову намотування дроту діаметром 0,2 мм і по ньому тече струм 0,1 А. Довжина соленоїда 20 см, діаметр 5 см. Знайти енергію і об'ємну щільність енергії магнітного поля соленоїда.
Рішення . Енергія магнітного поля соленоїда. де індуктивність соленоїда,; магнітна постійна; n - число витків на 1 м довжини соленоїда, при щільній намотуванні; довжина соленоїда; площа перерізу соленоїда. тоді:
Густина енергії визначається за формулою:
Приклад 13. конденсатор ємністю 40 мкФ повідомлений заряд 0,3 мКл, після чого його замикають на котушку з індуктивністю 0,1 Гн. Нехтуючи опором контуру, знайти закони зміни напруги на конденсатор
торі і сили струму в ланцюзі.
Рішення . За відсутності провідникові вільні коливання в контурі описуються рівнянням
де циклічна частота коливань.
Рішення рівняння (1) має вигляд
де початкова фаза коливань. Оскільки в початковий момент часу заряд конденсатора. то і, отже,.
Напруга на конденсаторі
а сила струму в ланцюзі
Числові значення, вийдуть як: