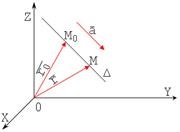
Рівняння прямої, що проходить через задану точку паралельно вектору має вигляд:
і називається векторно-параметричних рівнянням прямої. Тут - радіус-вектор довільної точки М (x, y, z) прямий; - радіус-вектор фіксованої точки. t - параметр, який приймає всілякі дійсні значення. Вектор називається напрямних вектором прямої. а його координати - напрямними коефіцієнтами прямий.
Якщо в рівнянні (1) перейти до координат векторів, то виходять параметричні рівняння прямої:
Якщо з рівнянь (2) виключити параметр t. то виходять канонічні рівняння прямої:
Пряму в просторі можна розглядати як лінію перетину двох площин
Т.ч. пряма визначається спільним завданням системи двох лінійних рівнянь:
Вони називаються загальними рівняннями прямої. В цьому випадку спрямовує вектор прямої можна визначити наступним чином:
Нехай задані дві прямі: і. Тоді умова паралельності прямих записується у вигляді:. умова перпендикулярності - у вигляді:. а кут між ними обчислюється за формулою
Рішення. а) Так як шукана пряма паралельна вектору. то цей вектор можна взяти за її направляючий вектор. Тоді канонічні рівняння шуканої прямої мають вигляд:
б) Так як шукана пряма паралельна прямій з напрямних вектором. то цей вектор паралельний шуканої прямої, значить, його можна прийняти за спрямовує вектор шуканої прямої. Тоді канонічні рівняння шуканої прямої мають вигляд:
в) Так як шукана пряма паралельна осі Ox. значить, вона паралельна вектору. тобто і канонічні рівняння шуканої прямої мають вигляд:
Випадок, коли хоча б в одному знаменнику канонічних рівнянь прямої виходить нуль, не позбавлене сенсу, але свідчить про те, що спрямовує вектор прямої має одну або дві нульові координати. У таких випадках краще записувати параметричні рівняння прямої:
Приклад 2. Скласти канонічні рівняння прямої
Рішення. Для складання канонічних рівнянь прямої необхідно знати спрямовує вектор і якусь фіксовану точку на прямій M0. Спрямовує вектор обчислимо як векторний добуток нормальних векторів площин, цю пряму утворюють. Оскільки . . то
Як фіксованою точки можна вибрати будь-яку точку прямої. Задамо одну з координат шуканої точки довільно. Нехай z = 0. тоді
Тепер складаємо канонічні рівняння прямої, знаючи її направляючий вектор і фіксовану точку M0.