1. Якщо площина, в якій розташований деякий кут, перпендикулярна до площини проекцій, то він проектується на цю площину проекцій у вигляді прямої лінії.
2.Якщо площину прямого місце не перпендикулярна до площини проекцій і хоча б одна його сторона паралельна цій площині, то прямий кут проектується на неї у вигляді прямого же кута.
Покладемо, що сторона СВ прямого кута АСВ (рис. 89) паралельна площині проекцій. В такому випадку пряма СВ паралельна С ° У °. Нехай друга сторона (АС) прямого кута перетинає свою проекцію А ° С ° в точці К. Проводимо в площині проекцій через точку К пряму паралельно С ° У °. Пряма KL також параллельпа СВ, і кут CKL виходить прямим. Згідно з теоремою про три перпендикуляри кут C ° KL - також прямий 1). Отже, і кут А ° С ° У ° - прямий.
1) Для точок, що належать перехресних прямих і розташованих на одній і тій же проецирующей прямий, зустрічається назва «конкуруючі».
До цієї теореми про проектування прямого кута відповідають дві зворотні (пп. 3 і 4).
3.Якщо проекція плоского кута є прямий кут, то проектується кут буде прямим лише за умови, що принаймні одна зі сторін цього кута паралельна площині проекцій.
4. Якщо проекція деякого кута, у якого одна сторона паралельна площині проекцій, являє собою прямий кут, то проектується кут теж прямий 2).
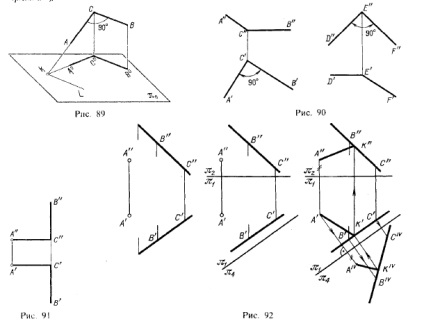
На підставі викладеного можна встановити, що кути, зображені на рис. 90, в просторі прямі.
В якому випадку проекції прямого кута на двох площинах проекцій є прямі кути? Це буває, коли одна сторона прямого кута перпендикулярна до третьої площини проекцій (тоді інша його сторона паралельна згой площині), Приклад дан на мал. 91: сторона АС перпендикулярна до π3. сторона ВС паралельна π3.
Користуючись відомостями про проектуванні прямого кута, про доповнення системи π1. π2 системою π4. π1 (§ 8) і про розташування проекцій прямої, паралельної одній з площин проекцій (§ 11), ми можемо виконати наступну побудову: провести через деяку точку А пряму так, щоб вона перетнула дану пряму під-кутом 90 °, Рішення показано на рис , 92, де зліва дано вихідне положення, в середині показано освіту, крім Системи 1. π2. ще однієї системи π4. π1. причому пл. кπ4 || ВС, а праворуч виконано побудова прямої АК⊥ВС.
1) Відповідно до прямої теореми про три перпендикуляри: якщо КL⊥С ° К, то KL.⊥СК. Згідно зворотної теоремі: якщо KL⊥СК, то KL⊥С ° К.
2) Тих, хто цікавиться доказом зворотних теорем відсилаємо до попередніх видань книги,
Так як пл. π3 || ВС, що забезпечується проведенням осі до pi; 4 / π1 паралельно В'С ', то прямий yгол АКВ (або AKCj проектується на пл. Pi; 4 у вигляді прямого же кута A IV K IV B IV Побудувавши проекції точки А і прямої ВС на пл. pi; 4. проводимо A IV K IV ⊥B IV C IV. а татем отримуємо проекції К 'і К "і проекції А'к' і а" К "(хід побудови вказано стрілками).
Чи можна вважати, що. побудувавши перпендикуляр АК до прямої ВС, ми визначили відстань від А до ВС? Ні, ми тільки побудували проекції відрізка АК; жодна з них не визначає величини відстані. Якщо треба визначити величину відрізка АК, т. Е. Відстань від А до ВС, то треба продовжити побудову, застосувавши хоча б спосіб, викладений у § 13.
5. Якщо площину тупого або гострого місце не перпендикулярна до площини проекцій і хоча б одна сторона кута паралельна площині проекцій, то проекція тупого кута на цю площину є тупий кут, а проекція гострого кута - гострий кут.
Припустимо, що пряма СВ (рис. 93) паралельна площині проекцій. Розглянемо тупий кут КСВ або гострий кут МСВ і проведемо в площині цією кута пряму CL⊥СВ. Так як кут LCB - прямий, то його проекція - кут LС ° В °
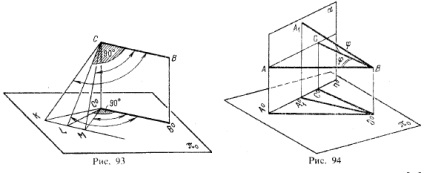
є також прямий кут. Цей кут міститься всередині кута КС ° В ° і містить в собі кут МС ° В °, отже, кут КС ° В ° - тупий, а кут МС ° В ° - гострий. Таким чином, проекція кута є кут з тією ж назвою (прямий, тупий або гострий), що і сам кут, якщо хоча б одна сторона кута паралельна площині проекцій. Взагалі ж проекція будь-якого кута може являти собою або гострий, або прямий, або тупий кут, в залежності від положення кута відносно площини проекцій.
6. Якщо обидві сторони будь-якого кута паралельні площині проекцій, то його проекція дорівнює за величиною, яка буде проектуватися кутку.
Це випливає з рівності кутів з паралельними і однаково спрямованими сторонами.
Тому, наприклад, кут між прямою АВ (рис. 50, с. 27) і пл. π2 легко визначити: его - кут між проекцією А'В 'і віссю х; таким же чином кут між CD і пл. π1 (рис. 51) визначиться як кут між C "D" і віссю х, кут між ЕF (рис. 52) і пл. π2 - як кут між E " 'F"' і віссю z.
Для прямого кута рівність між його проекцією і самим кутом має .песта і тоді, коли лише одна сторона прямого кута паралельна площині проекцій.
Але для гострого або тупого кута, у якого одна сторона паралельна площині проекцій, проекція кута не може дорівнювати проецируемую кутку. При цьому проекція гострого кута менше проектованого кута, а проекція тупого більше проектованого кута.
Нехай (рис. 94) кут А 1 ВС - гострий і нею сторона СВ паралельна пл. π0; З ° В ° || СВ. Пл. проведена через точку С перпендикулярно до СВ, перпендикулярна до пл. π0. перетинаючи останню по прямій n °, проходить через С ° і перпендикулярної до С ° У °. Якщо провести через точку В різні прямі під тим же самим гострим кутом до прямої СВ, то всі ці прямі будуть перетинати пл. в точках, проекції яких розташуються на прямий п °. Покладемо, що прямі АВ і А1 В складають з прямою СВ рівні між собою кути: ∠ АВС = ∠А1 ВС. Якщо при цьому АВ паралельна площині π0. то ∠ А ° В ° С ° - ∠ АВС. Якщо ж сторона А1 В не паралельна π0. то проекція точки 'А1 вийде на прямий n ° ближче до С °, ніж проекція точки А. Отже, проекція кута А1 ВС є кут, менший кута А ° В ° С °, т. е. ∠А ° В ° С ° 1).
9.Еслі боку кута однаково нахилені до площини проекцій, то кут-проекція не може дорівнювати проецируемую кутку
Це (рис. 95) можна встановити шляхом поєднання кута MKN з пл.π0 при обертанні навколо прямої MN. При цьому кут MK ° N виявиться всередині кута MK1 N, а вершини К1 і К ° - на загальному перпендикуляре до MN.
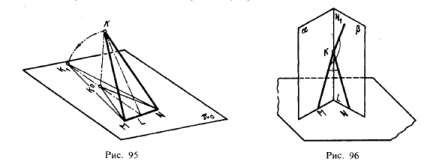
9.Проекціі гострого і тупого кутів можуть дорівнювати проецируемую кутку не тільки за умови паралельності сторін кута площини проекцій.
З рис. 96 видно, що всі кути, наприклад гострий кут MKN і тупий кут MKN1. боку яких відповідно розташовані в проектують площинах. і. мають своєї проекцією кут, рівний куту MLN, причому ці кути можуть наближатися до 0 ° і до 180 °. Очевидно, серед цих кутів може виявитися кут, рівний своїй проекції.
Приклад побудови такого кута дан в § 38.
Питання до §§ 13-15
- Як побудувати на кресленні прямокутні трикутники для визначення довжини відрізка прямої лінії загального положення і її кутів з площинами проекцій π1 і π2?
- Яким умовам повинні відповідати кути між прямою загального положення і площинами проекцій π1 і π2?
- Яка властивість паралельного проектування відноситься до паралельних прямих?
- Чи можна за кресленням двох профільних прямих в системі π1, π2 визначити, паралельні між собою ці прямі?
- Як зображуються в системі π1, π2 дві пересічні прямі лінії?
- Як випливає тлумачити точку перетину проекцій двох перехресних прямих?
- В якому випадку прямий кут проектується у вигляді прямого кута?
- В якому випадку проекція тупого або гострого кута обов'язково є кутом з тією ж назвою (тупий або гострий)?
- Чи може проекція гострого або тупого кута, у якого одна сторона паралельна площині проекцій, дорівнювати самому кутку в просторі?
- В якому випадку розподіл проекції кута навпіл відповідає такому розподілу самого кута в просторі?
- Чи може кут-проекція на деякій площині проекцій дорівнювати проецируемую кутку, сторони якого складають з цією площиною рівні кути?
- Чи може гострий або тупий кут, сторони якого не паралельні площині проекцій, рівнятися своєї проекції на цій площині?