На дослідницьку роботу «Пані Симетрія», виконану учням 5А класу МБОУ «ЗОШ № 10» м Усолье-Сибірське Алтунина Володимиром.
Поняття симетрії зустрічається як у багатьох сферах людського життя, культури і мистецтва, так і в сфері наукових знань. Але що таке симетрія? У перекладі з давньогрецької мови це - відповідність, незмінність, відповідність. Говорячи про симетрії, ми часто маємо на увазі пропорційність, впорядкованість, гармонійну красу в розташуванні елементів якоїсь групи або складових якогось предмета.
Алтунин В. розібрався з найпростішими типами просторової симетрії: дзеркальної (породженої відображеннями); осьової; центральною.
Матеріал про симетрії він знайшов в інтернеті і енциклопедії. Знайшов приклади симетрії в природі, архітектурі, техніці, в побуті, хімії.
Володимир виконав ряд практичних завдань: намалював малюнки з центральної і осьової симетрією, сфотографував кілька будівель в м Усолье-Сибірське, С-Петербурзі, визначив симетричні точки; склав кросворд.
Дана робота може бути використана на факультативному занятті в 5-6 класах.
Поняття симетрії зустрічається як у багатьох сферах людського життя, культури і мистецтва, так і в сфері наукових знань. Але що таке симетрія? У перекладі з давньогрецької мови це - відповідність, незмінність, відповідність. Говорячи про симетрії, ми часто маємо на увазі пропорційність, впорядкованість, гармонійну красу в розташуванні елементів якоїсь групи або складових якогось предмета.
Симетрія відносно осі або лінії перетину площин називається осьової. Вона передбачає, що якщо через кожну точку осі симетрії провести перпендикуляр, то на ньому завжди можна знайти 2 симетричні точки, розташовані на однаковій відстані від осі. У правильних багатокутниках осями симетрії можуть бути їх діагоналі або середні лінії. У окружності осі симетрії - її діагоналі.
Симетрія відносно точки називається центральної. У цьому випадку на рівній відстані від точки по обидві її сторони знаходяться інші точки геометричні фігури, прямі або криві лінії. При з'єднанні симетричних точок прямої, що проходить через точку симетрії, вони будуть розташовані на кінцях цієї прямої, а серединою її з'явиться якраз точка симетрії.
Дзеркальна симетрія, це вид симетрії, часто спостерігається в природі і в створених людиною речей, - так звана дзеркальна симетрія.
Симетрія в природі, техніці, архітектурі, хімії, в побуті.
II. Симетрія (теоретична частина)
2) Центральна симетрія ......................................................
3) Дзеркальна симетрія .........................................................
4) Симетрія в природі ......................................................
5) Симетрія в техніці .........................................................
7) Симетрія в архітектурі ......................................................
III. Симетрія (практична частина) ...........................................
Вивчити найпростіші типи просторової симетрії (центральну, осьову, дзеркальну)
Вивчити явища симетрії в зоології, ботаніки, архітектурі, транспорті і техніці, хімії, побуті.
Створити ілюстративний комп'ютерний і свій матеріал з усіх розділів дослідження симетрії: в зоології, ботаніки, архітектурі, техніці, хімії, побуті.
Скласти кросворд, буклет.
Сфотографувати приклади симетрії в побуті, архітектурі
П'ятикласників під силу зрозуміти і засвоїти цю тему.
Методи дослідницької роботи:
Збір і структурування зібраного матеріалу на різних етапах дослідження.
Виконання малюнків, креслень; фотографій.
Передбачуване практичне застосування: використання результатів дослідження у вигляді презентацій вчителями - предметниками, в якості допоміжного матеріалу при проведенні факультативних занять.
Поняття симетрії зустрічається як у багатьох сферах людського життя, культури і мистецтва, так і в сфері наукових знань. Але що таке симетрія? У перекладі з давньогрецької мови це - відповідність, незмінність, відповідність. Говорячи про симетрії, ми часто маємо на увазі пропорційність, впорядкованість, гармонійну красу в розташуванні елементів якоїсь групи або складових якогось предмета.
Поняття симетрії фігур з'явилося в результаті спостережень над об'єктами навколишнього світу. Наприклад, розглядаючи зображення рослин і тварин організмів, можна переконатися, що багато хто з них з великим ступенем точності володіють тією або іншою симетрією. Так, лист клена має осьову симетрію. Різними видами симетрії мають квіти, багато живі організми - морські зірки, метелики. Симетрією обертання і осьовими симетрії мають сніжинки.
З симетрією ми часто зустрічаємося в мистецтві, техніці, побуті. Наприклад, симетричні фасади багатьох будівель і їх види зверху. Симетричні візерунки на килимах, візерунки бордюрів, багато видів механізмів, наприклад колесо або шестерня.
Що таке осьова симетрія?
Симетрія відносно осі або лінії перетину площин називається осьової. Вона передбачає, що якщо через кожну точку осі симетрії провести перпендикуляр, то на ньому завжди можна знайти 2 симетричні точки, розташовані на однаковій відстані від осі. У правильних багатокутниках осями симетрії можуть бути їх діагоналі або середні лінії. У окружності осі симетрії - її діагоналі.
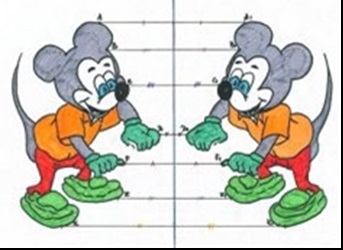
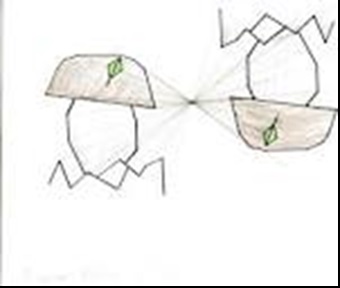
Симетрія відносно прямої (осі симетрії) передбачає, що по перпендикуляру, проведеним через кожну точку осі симетрії, на однаковій відстані від неї розташовані дві симетричні точки. Щодо осі симетрії (прямий) можуть розташовуватися ті ж геометричні фігури, що і відносно точки симетрії.
Прикладом може служити лист зошити, який зігнутий навпіл, якщо по лінії згину провести пряму лінію (вісь симетрії). Кожна точка однієї половини аркуша матиме симетричну точку на другій половині листа, якщо вони розташовані на однаковій відстані від лінії згину на перпендикуляр до осі.
Що таке центральна симетрія?
Симетрія відносно точки називається центральної. У цьому випадку на рівній відстані від точки по обидві її сторони знаходяться інші точки геометричні фігури, прямі або криві лінії. При з'єднанні симетричних точок прямої, що проходить через точку симетрії, вони будуть розташовані на кінцях цієї прямої, а серединою її з'явиться якраз точка симетрії. А якщо обертати цю пряму, закріпивши точку симетрії, то симетричні точки опишуть криві так, що кожна точка однієї кривої лінії буде симетрична такий же точці інший кривої лінії.
Симетрія відносно точки передбачає, що по обидва боки від точки на однакових відстанях знаходиться що-небудь, наприклад інші точки або геометричне місце точок (прямі лінії, криві лінії, геометричні фігури).
Якщо з'єднати прямою симетричні точки (точки геометричної фігури) через точку симетрії, то симетричні точки лежатимуть на кінцях прямої, а точка симетрії буде її серединою. Якщо закріпити точку симетрії і обертати пряму, то симетричні точки опишуть криві, кожна точка яких теж буде симетрична точці інший кривої лінії.