Спочатку коротко теорії.
Прості числа це натуральні числа які діляться тільки на себе і на одиницю. 2,3,5,7,11,13,17,19,23,29.
Головна складність простих чисел полягає в тому, що їх не так просто знайти коли мова йде про гігантський значеннях. Все тому що немає достатньо простої формули для обчислення їх послідовності. Наприклад найбільше знайдене просте число, на сьогоднішній день, має 22 338 618 цифр, за обсягом це приблизно 7 томів війна і мир.
Іноді знічев'я я намагаюся знайти формулу яка б знаходила прості числа, та заняття так собі, але ця як жуйка для мізків, марно, але мозок думає, вважає. І все ж, можливо я здається знайшов спосіб знаходження цих самих чисел простіше. Слов "можливо" це тому, що мені не вистачає достатньо математичних і комп'ютерних знань, що б це перевірити, тому і хочу поділитися тим що є. Може хто зможе до формулювати мою думку, щоб переглянути цей спосіб.
Загалом суть поста. Я вирішив вивести банальну послідовність з окремих послідовностей самих простих чисел і записав це в вигляді табличці, де кожне просте число має послідовність у вигляді: 2 = (1,2,1,2,1,2.) 3 = (1,1, 2,1,1,2,1,1,2.) 5 = (1,1,1,1,5,1,1,1,1,5,1,1,1,1,5.) і т.д. Спочатку вийшла така ось табличка.
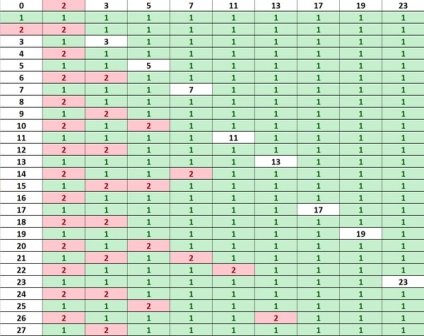
Вийшло, що в лініях де все "1" виходить нове просте число. Далі трохи спростив табличку, замінив 1 на 0, 2 на 1, в принципі без різниці який вигляд матиме послідовність (1,1,2,1,1,2) або (0,0,1,0,0,1) , здалося так по простіше буде. І прибрав 2 і парні числа, оскільки вони все одно не потрапляють під парні.
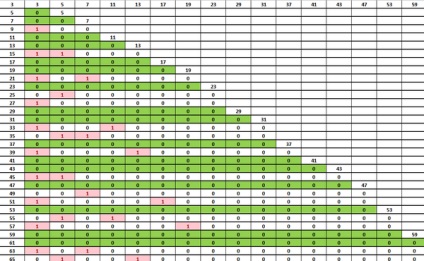
В принципі ця таблиця показує очевидні речі, три - ділить кожне третє число, п'ять - кожне п'яте, сім - кожне сьоме. зате видно, що б знайти таке просте число, достатньо, щоб був тільки 0 на лінії, і напевно навіть можна зробити формулу (є схожі, але немає саме з перетин послідовностей), але це буде все одно безглуздо оскільки для великих чисел обчислення буде нескінченно довгим.
Інша справа сама табличка. Мені здається (і можливо тільки здається і я не маю рації) що можна зробити програму яка буде обчислювати таку табличку, адже тут в принципі немає особливих обчислення. Є дуже легкі послідовності, напевно можна задати програмі яка буде писати в стовпець кожне задане число 1 замість 0, і перевіряти рядок, якщо всюди 0, то задає собі ж новий стовпець. Так, для великих чисел буде неймовірно великий обсяг даних, але наприклад для того ж простого числа з 22 338 618 цифр, на перевірку його простоти пішло 2 роки.
Загалом мені просто дуже цікаво, чи можна зробити таку таблицю що б вираховувала сама себе? (Якщо немає то, вибачте за витрачений час), і якщо можна, чи не буде це більш швидким способом обчислення простих чисел?
Можливо є серед пікабушніков: математики, програмісти, хто зможе перевірити.
1. Зробити "таблицю" можна.
2. Швидше не буде - навіть банальна перевірка великих чисел на простоту перебором від 2 до квадрата цього числа (немає сенсу перевіряти від 2 до самого числа - 1) і порівняння залишку від ділення буде швидше, ніж заповнення таблиці. Тест Люка-Лемера, просто додаючи до n + = 2 повинен відпрацювати ще швидше. Але, можливо, варто вигнати тести - тільки потрібно визначитися з доступним об'ємом ОЗУ (самі розумієте, що зчитувати значення ліній з файлу буде гальмувати процес багаторазово).
Якщо є бажання - можу допомогти з кодом на Python * він мені цікавіше * або сі * тут арифметика повинна буде працювати трохи швидше * (з поясненням, що до чого, що б, в кінці, могли писати самі). Від excel-a доведеться йти відразу, тому що гальмувати буде сам office і адекватно оцінити час розрахунку по таблиці і перебором не зможете.
p.s. Поставлю + за пост - було цікаво прочитати.
Розкрити гілка 0
Щось мені підказує, що це не "алгоритм", а просто візуалізація поняття "просте число".
Розкрити гілка 0
Взагалі чув, що прості числа мають якийсь зв'язок з числами Фібоначі
Розкрити гілка 0
Ти отримав якийсь дивний "спрощення" канонічного виду натурального числа.
Очевидно що якщо в канонічному вигляді числа є тільки саме число, то воно просте