18. Прямокутна коробочка з жерсті масою m = 76 г з дном площею S = 38 см 2 і висотою H = 6 см плаває у воді. Визначте висоту h надводної частини коробочки.
Рішення. Коробочка плаває, якщо діюча на неї сила тяжіння дорівнює по модулю діючої на неї сили Архімеда: mg = FА. причому FА = Vпчg ρв. де - обсяг зануреної частини коробочки. Підставляючи числові дані, отримуємо
Звідси глибина занурення коробочки дорівнює
Значить h = H - x = 4 см.
19. Крижина плаває на поверхні прісної води. Яку частину становить обсяг підводної частини від обсягу всієї крижини? Якщо завдання не вирішується в загальному вигляді, то, для спрощення, прийміть обсяг крижини рівним 100 м 3. Щільність льоду 900 кг / м 3.
Рішення. Раз крижина плаває, то її сила тяжіння дорівнює по модулю силі Архімеда: mg = FА. т. е .:
20. На поверхні широкого озера лід має товщину 2 м. Який мінімальної довжини треба взяти мотузку, щоб зачерпнути кухлем води з ополонки?
Рішення. Так як озеро широке, то лід на його поверхні може тільки плавати, а не триматися за берега за рахунок примерзання до них. Згідно з рішенням завдання № 19, в ополонці під поверхнею води виявиться 0,9 товщі льоду, т. Е. 0,9 · 2 м = 1,8 м, а над поверхнею води 0,2 м = 20 см. Для зачерпиванія води з такої глибини мотузка не потрібна.
21. У склянці з прісною водою плаває шматок льоду. Чи зміниться рівень води, коли лід розтане? Розгляньте додатково випадки: коли в лід вмёрзла дробинка; коли в лід вмёрз бульбашка повітря.
Рішення. Лід плаває, якщо його вага дорівнює вазі рідини в об'ємі зануреної частини. Новоутворена з льоду прісна вода має ту ж вагу, що і лід, і, отже, точно заповнить обсяг, який витісняв плаваючий лід. Значить, рівень води не зміниться.
Якщо в льоду була дробинка, лід витісняв більше води, щоб підтримувати на плаву дробинку. Коли лід розтанув, дробинка потонула (її вага більше ваги витісненої нею води), рівень води знизився.
У разі вмёрзшего бульбашки рівень води після танення криги практично не зміниться. Хоча, якщо підрахувати точно, рівень води дещо знизиться, т. К. Маса повітря в бульбашці хоч і мала, але не дорівнює нулю.
Рішення. Вага судини при опусканні в нього моделі збільшиться на вагу моделі mg. Це збільшення ваги можна інтерпретувати як наслідок підйому рівня води на Δh і, отже, збільшення сили тиску води ΔFд = ρвg ΔhS. Звідси:
23. Шматок парафіну масою m = 200 г плаває на межі поділу води і бензину. Визначте обсяг V1 надводної частини бруска. Щільність парафіну 900 кг / м 3. бензину 700 кг / м 3.
Рішення. Якщо парафін плаває, то сила тяжіння дорівнює сумі сил Архімеда в обох рідинах: mg = Vв ρвg + V1 ρбg. де Vв - об'єм, занурений у воду, V1 - шуканий надводний обсяг (в бензині). Загальний обсяг парафіну
Вирішуючи спільно обидва рівняння, отримуємо:
24. Шматок льоду, всередину якого вморожени кульку зі свинцю, плаває в циліндричній посудині з водою. Площа дна посудини S. Яка маса кульки, якщо після повного танення льоду рівень води в посудині знизився на H. Щільність свинцю ρ1. щільність води ρ2.
Рішення. На плаваючу крижину з свинцевим кулькою діє більша сила Архімеда, ніж на таку ж крижину без кульки, т. К. Вона важча на силу тяжіння кульки mg. Отже, обсяг витісняється в першому випадку води більше, ніж у другому, на Але коли крижина розтане, кулька впаде на дно і займе обсяг V1 = m / ρ1. Загальне зменшення обсягу води в кінцевому рахунку ΔV = ΔVп - V1. Так як ΔV = SH (за умовою), то приходимо до рівняння:
25. Корона царя Гієрона в повітрі важить P1 = 20 Н, а у воді P2 = 18,75 Н. Обчисліть щільність речовини корони. Чи була вона з чистого золота? Доповнення: знайдіть, скільки золота і скільки срібла було в короні. Щільність золота округлено прийняти 20 000 кг / м 3. а срібла 10 000 кг / м 3.
- корона не з чистого золота.
Щоб визначити склад корони, використовуємо два факти: 1) загальна маса корони m = mз + mс; 2) загальний обсяг корони V = Vз + Vс (індекси «з» і «с» відносяться до золота та срібла відповідно). Замінюючи обсяги їх виразами через маси і щільності, отримуємо систему з двох рівнянь:
Опускаючи громіздкі проміжні обчислення, запишемо відповідь:
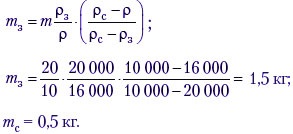
26. Яку силу треба прикласти до коркового тілу масою 400 кг, щоб утримувати його, коли воно цілком занурене у воду? ρп = 200 кг / м 3; g = 10 м / с 2.
Рішення. Сила тяжіння тіла mg = 4000 Н спрямована вниз, сила Архімеда спрямована вгору і дорівнює
Щоб утримати тіло в воді, треба докласти спрямовану вниз силу F = FА - mg = 16 кН.
27. Чавунна плита товщиною 0,5 м, довжиною 10 м і шириною 4 м лежить на глинистому дні, видавивши з-під себе воду. Глибина водойми 2,5 м. Яку силу необхідно прикласти, щоб почати підйом плити?
Рішення. Обсяг плити V = 0,5 м х 10 м · 4 м = 20 м 3.
Її маса m = V ρч = 20 м 3 · 7000 кг / м 3 = 140 000 кг.
Сила тяжіння mg = 1 400 000 Н.
Оскільки під плитою немає води, сила Архімеда на неї не діє. Вниз на плиту, крім сили тяжіння, діють сила тиску води на глибині 2,5 - 0,5 = 2 (м) і сила тиску атмосфери, яку передає вода за законом Паскаля. При нормальному атмосферному тиску загальний тиск на плиту:
Горизонтальна площа поверхні плити S = 40 м 2. Сила тиску на плиту F = pS = 4,8 · 10 6 Н.
Повна сила, що притискає плиту до грунту:
F = mg + Fа = 1,4 · 10 6 Н + 4,8 · 10 6 Н = 6,2 · 10 6 Н.
Для відриву від ґрунту потрібна сила F> 6,2 МН.