Контрольна робота №1 З ПРЕДМЕТУ «ГЕОДЕЗІЯ»
ВАРІАНТШІФР Я (10) 56
Заданіе1 Відповіді на питання «Основні відомості з геодезії»
I.Сведенія про фігуру Землі. Застосовувані в геодезії системи координат. Орієнтування ліній.
Питання: Що називають географічним або істинним азимутом і дирекційний кутом? Яка залежність між прямим і зворотним дирекційний кутами даної лінії?
Орієнтувати лінію місцевості - значить знайти її напрямок щодо меридіана. Як кутів, що визначають напрямок ліній, служать азимути, дирекційні кути і румби.
Азимутом А називається горизонтальний кут, відрахований по ходу годинникової стрілки від се-вірною частини меридіана до заданого напрямку від 0 до 360 ° (рис.1) .Якщо азимут відраховується за годинниковою стрілкою від північного напрямку дійсного меридіана до заданого напрямку від 0 до 360 °, то такий азимут називається істинним, або географічним
Прямий азимут напрямку P1 P2 (див. Рис.1.) Буде A1. а об-ратний для того ж направ-лення - А2. Меридіани не паралельні між собою, тому азимут лінії в каж-дой її точці має різне значення. Кут між направ-лениями двох меридіанів в даних двох точках називаються ється зближенням меридіанів і позначається че-рез # 947; Як видно з рис 1, залежність між прямим і зворотним ази-мутамі лінії виражається формулою
Азимути як орієнтирні кутів застосовні на сфероїдічеськой або сферичної по-поверхні Землі. При зображенні земної поверхні на площині в будь-якої проекції, на-приклад Гаусса - Крюгера, користуються площинним орієнтирними кутом, називає-мим дирекційний.
Дирекційний кутом лінії на площині називається кут ме-жду зображеннями на ній осьового меридіана і заданий-ним напрямом по ходу годинникової стрілки від 0 до 360 °. Кути дирекцій позначити-ються буквою # 945 ;.
Як випливає з рис.2, зв'язок між азимутами і дирекційний кутами виражається форму-лій
де # 947; - зближення меридіанів в точці Р1. т. е. кут між зображеннями осьового меридіана і меридіана даної точки. При користуванні формулою треба мати на увазі, що зближення меридіанів то-чек, розташованих до по-стоку від осьового меридіана, має знак плюс, а до запа-ду - знак мінус. Прямий і зворотний дирекційні кути однієї і тієї ж лінії відрізняються на 180 ° і визначаються:
Якщо позначити різницю довгот даного меридіана і осьового через I, то зближення меридиа-нів буде свя-зано з різницею довгот наближеною формулою
де B - геодезична широта даної точки.
II.Общіе відомості про вимірювання і елементи математичної обробки результатів геодезичних вимірювань.
Питання: Що таке гранична похибка і як її визначають?
Види похибок вимірювань, їх класифікація вимірювання в геодезії розглядаються з двох точок зору: кількісної та якісної, що виражає числове значення виміряної величини, і якісною - характер її точність. З практики відомо, що навіть при самій ретельній і акуратною роботі багато кратні виміру не дають однакових результатів. Якщо позначити справжнє значення вимірюваної величини X а результат вимірювання l від справжня помилка виміру дельта визначається з виразу
Випадкові похибки характеризують слід властивостями. При визначенні умов вимірювання випадкові не можуть перевищувати певної межі, званого граничною похибкою. Це властивість дозволяє виявляти і виключати з результатів вимірів грубі помилки. Позитивні і негативні помилки приблизно однаково часто зустрічаються в ряду вимірів, що допомагає виявленню систематичних помилок. Чим більше абсолютна величина помилки, тим рідше вона зустрічей в ряді вимірювань. Середнє арифметичне з випадкових помилок вимірів однієї і тієї ж величини, виконаних при один умовах, при необмеженому зростанні числа вимірів прагне до 0. це властивість компенсації. Остання властивість випадкових помилок дозволяє встановити принцип отримання з ряду вимірювань однієї і тієї ж величини результату, найбільш близького до її істинного значення т е. Найбільш точного. Таким результатом є середнє арифметичне з n виміряних значень цієї величини. При нескінченно великому числі вимірювань n lim (l | n) = X точність остаточного результату тим вище чим більше n для правильного використання результатів вимірювань необхідно знати з якою точністю - з яким ступенем близькості до істинного значення вимірюваної величини, вони отримані. Характеристикою точності окремого виміру в теорії помилок служить запропонована Гауссом середня квадратична помилка m, обчислена за формулою де n число вимірювань даної величини. Ця формула може бути застосована для випадків, коли відомо істинне значення вимірюваної величини. Такі випадки в практиці зустрічаються рідко. У той же час із вимірів можна отримати результат, найбільш близький до істинного значення - ари середину. Середньо квадрат помилка підчитують по ф Бесселя де - відхилення окремих значень вимірюваної величини від ари середини, звану вероятнейшими помилками. Точність ари середини природно вище точності окремого виміру.
III. лінійні вимірювання
Питання: Який принцип вимірювання відстаней нитяним далекоміром? Напишіть робочу формулу.
Далекомірні визначення відстаней
Ідея оптичних далекомірів заснована на рішенні трикутника (прямокутного або рівнобедреного), в якому по малому (параллактическому) кутку р і про-тіволежащей йому сто-Рона (базису) визначають расстоя-ня D за формулою
Одна з величин (кут # 946; або базис b) постійна, іншу вимірюють. Відповідно до цього застосовують далекоміри з постійним кутом і змінним базисом або з постійним базисом і змінним кутом.
Нитяний далекомір є далекоміром з посто-янним кутом і змінним базисом, ко-менту, котрим служить нівелірна рейка, вертикально встановлюється на кон-це відрізка, довжину якого оп-чати. Далекомір складається з двох горизонтальних ниток, паралельних середньої горизонтальної нитки сітки зорової труби геодезичного інструменту (теодоліт, нівелір,). Для вимірювання відстані на одному кінці відрізка встановлюють інструмент, на іншому - нівелірну рейку.
Коефіцієнт далекоміра зазвичай буває рівним 100, тому дальномерний відлік по рейці в сантімет-рах висловить шукане відстань в метрах.Дальномерние нитки сітки повинні розташовуватися на однаковій відстані від середньої горизонтальної нитки, що перевіряють по різниці відліків по рейці за трьома ні-тям: середня з від-рахунків по крайнім ниткам має сов-падати з відліком по середній нитці (розбіжність отсч-тов до 3 - 4 мм).
Незалежно від паспортних даних інструменту сле-дует визначати коефіцієнт далекоміра. Для цього на рівній місцевості вибирають лінію довжиною приблизно 100 м, початок її відзначають точкою, над якою центри-ють інструмент. Далі в створі лінії відкладають від початкової точки величину, постійного доданка з (рівну для труб з внутрішньої фокусується-кою, 0,1 м) і від цієї другої точки відміряють відстані, рівні 20, 40, 60, 80 і 100 м. Потім визначають ці відкладені відстані по далекоміру двічі, отримуючи далекомірної відстань як середнє значення з двох визна-лений.
Порівнюючи дальномірні відстані з фактично відміряними, обчислюють п'ять зна-чень коефіцієнта К, а за остаточне значення приймають середнє арифметичне.
При значному відхиленні, значення К. від 100 це-лесообразно (для знімальних робіт) до даного дально-міру виготовити свою рейку, для чого потрібно встановити заґрунтовану рейку на зазначеному раніше, відстані 100 м, відзначити на ній проекції віддалемірних ниток і розділити отриманий інтервал (умовний метр) на 100 рівних частин. Такі ж ділення сле-дует продов-жити і на інших частинах загрунтованной рейки. Відносна похибка визначення відстаней нитяним далекоміром становить приблизно 1: 300 вимірюваного відстані.
Вимірюючи далекоміром відстань між двома точ-ками, отримують довжину відрізка, на-лень до горизонту під деяким кутом, якщо кут нахилу переви-щує 1 ° 30 ', необхідно відлічене по далекоміру відстань привести до горизонту.
Робоча формула визначення відстані нитяним далекоміром, буде наступна:
Де К-коефіцієнт далекоміра, а с- постійний доданок.
При вимірі похилих відстаней горизонтальне прокладання визначають:
v - кут нахилу візирної осі зорової труби.
Питання: В чому сутність прямий і зворотної геодезичної завдань?
Пряма геодезична задача
Для вирішення геодезичних завдань в будівництві найбільш це-лесообразной є система прямокутних координацію-нат в проекції Гаусса-Крюгера. Для визначення координат наступних точок при відомих координатах початкової точки, відомих рас-стояння між точками і відомих дирекційних уг-лах сторін між точками вирішується пряма геодезичних-чна завдання.
Нехай маємо точку А з координатами XA і YA. а ко-ординати точки В 'позначимо через Х'B і Y'B (рис3). Проведемо через точку A лінію, паралельну осі абсцис, а через точку В '- лінію, паралельну осі ординат. В результаті отримаємо прямокутний тре-кутник, катети якого будуть рівні різницям координат:
величини # 916; х і # 916; y називаються приростами координат.
знаючи значення # 916; х і # 916; y боку АВ 'і координати
початкової точки А, можна визначити координати ко-кінцевих точки В '
Інакше кажучи, координата точки піду щей дорівнює координаті точки перед-дущей плюс відповідне прирощення, т. Е. В загальному випадку:
Залежно від напрямку боку АВ 'пріращена-ня координат # 916; х і # 916; у можуть мати знак плюс або знак мінус. Знаки збільшень координат визначають по на-правлінням сторін, т. Е по їх дирекційний кутах.
З рис. видно що: # 916; х = dcos # 945; # 916; y = dsin # 945;
З розгляду (рис.4) слід, що збільшення # 916; х і # 916; у координат є не що інше, як ортогональні проекції горизонтального відстані d між точками A і B 'і іншими на осі координат. Формули є формулами рішення прямої геодезичної за-дачі. Знаки прир-щений координат збігаються зі знака-ми тригонометричних функцій (відповідно синуса і косинуса дирекційного кута).
Збільшення координат можуть бути обчислені тре-ма способами: за таблицями натурал-них значень три-гонометріческіх функцій; за таблицями логарифмів і за спеціальними таблицями для обчислення збільшень координат, правила користування, якими викладено в пояс-неніі до таблиць.
У практиці геодезичних робіт для будівництва доводиться визначати координати не який-небудь однієї точки, а ряду точок, пов'язаних між собою горизон-тальне додатку-нями між точками і дирекційний кутами сторін, укладених між цими точками.
Зворотній геодезична завдання
У практиці будівництва вельми часто доводиться визначати довжину сторони і її ді-рекціонний кут по відомих координатах її кінцевих точок, т. Е. Вирішувати зворотня ву геодезичну задачу. Така заду-ча виникає при проектуванні і перенесеної-сеніі об'єктивним тов будівництва на місцевість.
Якщо відомі координати двох точок B 'і А (див. Ріс4.), Т. Е. Відомі збільшення ко-ординат по сторо-ні АВ', то тангенс дирекційного кута сторони АВ 'визначається з тре-кутника АВ "В':
З формули можна написати:
D = √ (Xb'-Xa) 2 + (Yb'-Ya) 2 = √ # 916; x 2 + # 916; y 2
При вирішенні зворотних геодезичних завдань користуються п'ятизначними таблицями логарифмів. Для визна-ділення величини дирекційного кута чверть устанав-ливают по знакам збільшень координат.
При наявності малих обчислювальних машин і значи-тельно кількості завдань рішення їх раціональніше виконувати нелогаріфміческім способом, користуючись п'ятизначними таблицями на-натуральній значень ТРИГОН-метричних функцій.
Заданіе2 Рішення задач
Завдання 1 Визначити дирекційні кути ліній ВС і СД, якщо:
Завдання 2 Визначити прямокутні координати точки Д, якщо:
Х (С) = (- 14,02м) + (cos46гр41мін х 239,14м) = (-14,02м) + (239,14м х 0,68949) = 150,865м
У (С) = 627,98м + (sin46гр41мінмін х 239,14м) = 627,98м + (239,14м х 0,72429221172333114981112266078498) = 753,433м
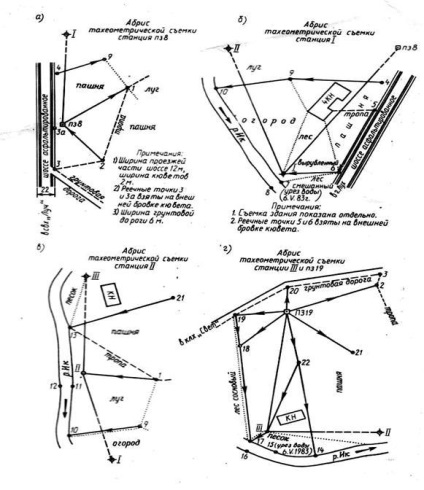
Завдання 3. Складання топографічного плану будівельного майданчика
Робота складається з наступних етапів: обробка тахеометрического журналу; побудова топографічного плану.
1. Для зйомки ділянки на місцевості між двома пунктами полігонометрії П38 і П319 був прокладений теодолітно-висотний хід. У ньому виміряні довжини всіх сторін а на кожній вершині ходу - правий по ходу горизонтальний кут і кути нахилу
на попередню і наступну вершини.
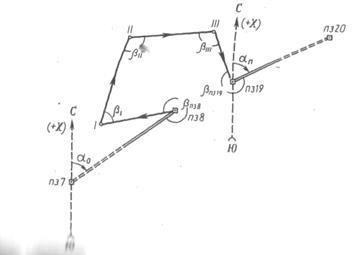
Результати вимірювань горизонтальних кутів і ліній (табл.2), а також тригонометричного нівелювання (табл.4 і 4а) є загальними для всіх варіантів.
Таблиця 2. Результати вимірювань кутів і довжин сторін ходу
Відомі координати полигонометрических знаків ПЗ 8 і ПЗ 19 (тобто початкової і кінцевої точок ходу):
Обчислення дирекційних кутів і румбів сторін ходу. За вихідним дирекційного кутку а 0 і виправленим значенням кутів b ходу за формулою для правих кутів обчислюють дирекційні кути всіх інших сторін: дирекційний кут наступної сторони дорівнює дирекційного кутку попередньої сторони плюс 180 ° і мінус правий (виправлений) кут ходу, утворений цими сторонами.
а ПЗ 8-1 = a 0 + 180 ° - bПЗ 8C = = 236гр 40,2мін.-189гр59,2мін = 46гр41мін
Для контролю обчислення дирекційних кутів слід знайти кінцевий дирекційний кут аn по дирекційного кутку а III-ПЗ 19 останньої сторони і виправленому куті bПЗ 19 при вершині ПЗ 19
Це обчислене значення аn має збігтися з заданим дирекційний кутом аn. При переході від дирекційних кутів а до румбам r см. Табл.1.
Значення дирекційних кутів записують в графу 4 відомості з точністю до десятих часток хвилин, а румбів - в графу 5; при цьому значення румбів округлюють до цілих хвилин.
Обчислення збільшень координат. Збільшення координат обчислюють за формулами:
D х = d cos a = ± d cos r; Dу = d sin a = ± d sin r
Заданіе4 Рішення задач за планом будівельної дільниці
Задача1 Визначення позначки точки лежить між горизонталями.
Нм.г. (відмітка меншою горизонталі) = 185
а (відстань до меншої горизонталі) = х 20 =
S (відстань між горизонталями) = м х 20 = м
Задача2 Визначення ухилу ВС