Обчислимо коефіцієнти аппроксимирующего полінома 3-го ступеня за методом найменших квадратів і представимо експериментально отриману залежність між х і y графічно.
З теоретичними відомостями, що стосуються полиномиальной апроксимації за методом найменших квадратів і реалізації цього методу засобами MathCad можна познайомитися в [20].
Напишемо програму на мові Паскаль, яка обчислює коефіцієнти аппроксимирующего полінома ступеня від 1 до 8. Щоб позбутися від ручного введення даних при налагодженні програми, збережемо через підрядник експериментальні значення аргументу і функції в текстових файлах Xi.txt і Yi.txt відповідно.
Вміст файлу Xi.txt матиме вигляд:
Вміст файлу Yi.txt:
Роздільником цілої та дробової частин повинна бути крапка. Файли Xi.txt і Yi.txt повинні бути поміщені в папку створюваної програми.
Основний алгоритм реалізуємо в окремій процедурі. Рішення системи лінійних алгебраїчних рівнянь щодо коефіцієнтів буде проводитися за методом Гаусса.
Таким чином, якщо точність коефіцієнтів обмежити трьома цифрами після коми, шукана апроксимуюча функція буде мати вигляд:
За допомогою даної програми можна обчислити коефіцієнти аппроксимирующего полінома і іншою мірою (неменшою 1 і не більшою 8) при іншій кількості експериментальних точок.
Аналогічну процедуру можна реалізувати і на Delphi.
Слід зауважити, що для обчислення
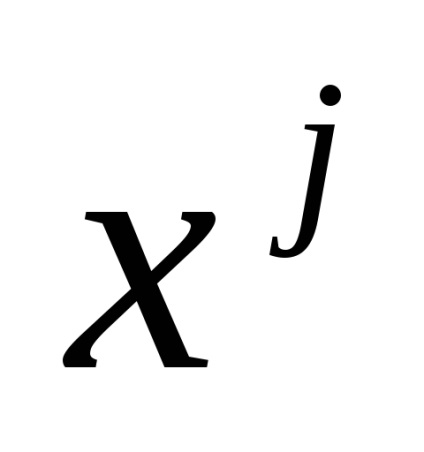
яка призводить до помилки при
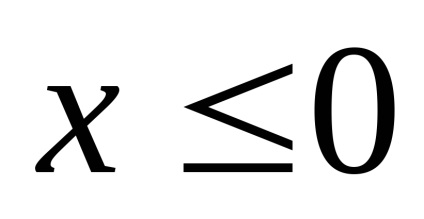
Оскільки ступінь, в яку зводиться величина х. в даній задачі - ціле число, то уникнути помилки можна, запровадивши додатковий цикл, в якому виконувалося б зведення величини х в ступінь шляхом множення самої на себе необхідну кількість разів.
Графік, знайденої функції (1), що містить і експериментальні точки, можна побудувати засобами Excel. Зразковий вид графіка, побудованого з кроком
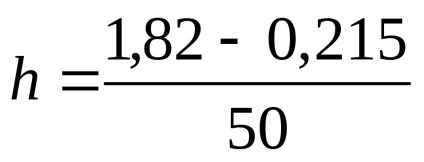
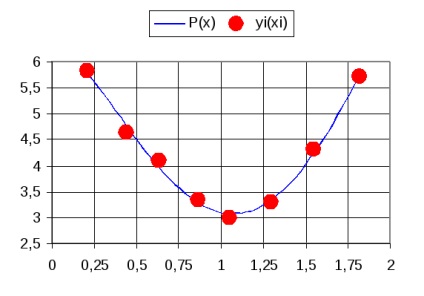
Малюнок 1 - Графік функції Р (х)