Область значень даної функції -це все числа, крім тих, коли знаменателеь звертається в 0.
Вирішуємо нерівність методом інтервалів.
Вирішуємо допоміжне рівняння.
Перенесемо відомі величини в праву частину рівняння.
Відповідь цього рівняння:
.
Відзначимо знайдені критичні точки і відповідні їм інтервали на числовій прямій.
Отримане рішення відзначимо на малюнку.
Для дослідження функції знайде першу похідну
Похідна твори константи і функції дорівнює добутку константи на похідну функції.
Скористаємося формулою похідної приватного.
Виносимо загальний множник.
Змінимо знаки виразів на протилежні.
Виносимо знак мінус з твору.
Друга похідна це похідна від першої похідної.
Похідна твори константи і функції дорівнює добутку константи на похідну функції.
Похідна твори константи і функції дорівнює добутку константи на похідну функції.
Скористаємося формулою похідної приватного.
Скористаємося властивістю ступенів.
Скористаємося формулою похідної твори.
Скористаємося правилом знаходження похідної для складної функції.
Розкриваємо дужки, використовуючи розподільний закон множення
Виносимо загальний множник.
Скористаємося властивістю ступенів.
Змінимо знаки виразів на протилежні.
Виносимо знак мінус з твору.
Точки перетину з віссю x:
Для знаходження точок перетину з віссю абсцис прирівняємо функцію до нуля.
Дріб звертається в нуль тоді, коли чисельник дорівнює нулю.
Розділимо ліву і праву частину рівняння на коефіцієнт при невідомому.
Точки перетину з віссю
:
Визначимо значення аргументу, при яких знаменник функції звертається в нуль
Перенесемо відомі величини в праву частину рівняння.
Похилі асимптоти: немає
Межа даної функції на нескінченності дорівнює числу 0
Для знаходження критичних точок прирівняємо першу похідну до нуля і вирішимо отримане рівняння.
Змінимо знаки виразів на протилежні.
Дріб звертається в нуль тоді, коли чисельник дорівнює нулю.
Отже, відповідь цього випадку:
.
Перенесемо відомі величини в праву частину рівняння.
Розділимо ліву і праву частину рівняння на коефіцієнт при невідомому.
Отже, відповідь цього випадку: немає рішень.
Можливі точки перегину: немає
Для знаходження можливих точок перегину прирівняємо другу похідну до нуля і вирішимо отримане рівняння.
Дріб звертається в нуль тоді, коли чисельник дорівнює нулю.
Ліва частина рівняння приймає тільки позитивні значення.
Відповідь: немає рішень.
Симетрія відносно осі ординат: функція парна, графік симетричний відносно осі
.
Функція f (x) називається парною, якщо f (-x) f (x).
Виносимо знак мінус з твору.
Симетрія відносно початку координат: немає
Функція f (x) називається непарною, якщо f (-x) -f (x).
Виносимо знак мінус з твору.
Наводимо подібні члени.
Проходячи через точку максимуму. похідна функції змінює знак з плюса на мінус.
Відносний максимум знаходиться в точці (0,0).
Дані таблиці нанесемо на координатну площину.
Використовуючи результати дослідження функції, побудуємо її графік.
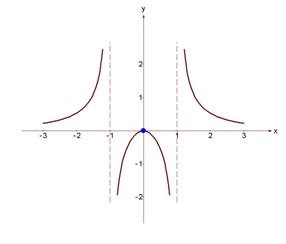
Безліч значень функції: безліч всіх дійсних чисел
Найменше значення і найбільше значення: у функції немає найменшого і найбільшого значення