Резервуванням називається спосіб підвищення надійності шляхом включення резервних блоків, здатних у разі відмови основного блоку виконувати його функції. Цей метод дає можливість отримання заданих рівнів надійності, і знайшов широке застосування в практиці.
У загальному випадку надійність не надмірною (НЕ резервованій) системи визначається як добуток надійності входять до неї елементів:
Це рівняння показує, що вихід з ладу будь-якого елемента призводить до відмови всього пристрою. Створення складних електронних пристроїв пов'язане із застосуванням широкого комплексу різних елементів, що розрізняються за своїми властивостями і характеристиками.
Поряд з високо надійними елементами в даний пристрій можуть входити і малонадійні, причому надійність НЕ зарезервованого пристрою не може перевищувати надійність самого ненадійного елемента.
Тому при синтезі високонадійних систем необхідно застосовувати резервування. Якщо є система з S паралельних елементів (рисунок 2.3), а ймовірність несправної роботи i-го елемента Qi. то ймовірність виходу з ладу системи
,
а ймовірність справної роботи
.
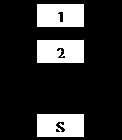
Малюнок 2.3 - Паралельне включення елементів
Отже, чим більше елементів S, тим більше надійність Р, тобто зі збільшенням числа резервних елементів надійність системи підвищується.
Різноманітні методи резервування і способи включення резерву можуть бути зведені до трьох методів резервування:
Загальним називається таке резервування, при якому паралельно включаються ідентичні системи, роздільним називають резервування систем шляхом застосування окремих резервних пристроїв, а при комбінованому - в одній і тій же системі застосовують загальне і роздільне резервування.
На малюнку 2.4 представлена система із загальним резервуванням.
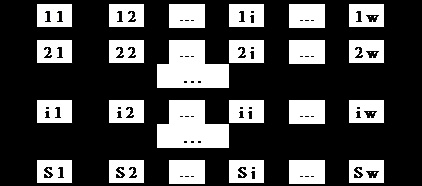
Малюнок 2.4 - Загальна резервування
На малюнку кожна система складається з w елементів, і паралельно підключено S систем.
При загальному резервуванні ймовірність відмови i-й дублюючої ланцюжка виражається наступною формулою
Рij - ймовірність справної роботи j-го елемента i-й ланцюжки.
При загальному резервуванні відмова системи виникне в разі відмови в основний і кожної резервної ланцюга. Звідси:
Імовірність справної роботи визначається за формулою: (32)
При однакових елементах (так само надійних)
де р - надійність кожного елемента.
На малюнку 2.5 представлена система з роздільним резервуванням.
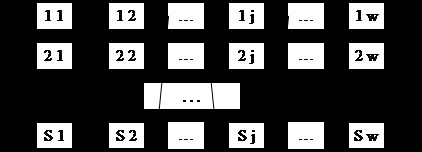
Малюнок 2.5 - Роздільне резервування
Якщо при роздільному резервуванні система складається з w елементів, кожен з яких має надійність Pj і являє собою S паралельно з'єднаних елементів, то надійність системи виражається наступною формулою:
Імовірність відмови умовного елемента:
,
де Qij - це ймовірність виходу з ладу i-го елемента j-ї групи.
Тоді формула надійності системи з роздільним резервуванням набирає вигляду:
При одно надійних елементах ця формула набуде вигляду:
Головним способом включення резервної апаратури при відмовах основний є наступні:
- постійне резервування, при якому резервні одиниці з'єднані з основними протягом всього часу роботи і знаходяться в однаковому з ними робочому стані;
- резервування заміщенням, при якому резервні одиниця заміщають основні тільки після відмови.
При цьому резервні одиниці можуть перебувати в 3-х режимах роботи:
1 навантажений (в гарячому резерві), при якому резервні одиниці знаходяться в тих же умовах, що і основні.
2 Чи не навантаженому (в холодному резерві), при якому резервна одиниця не включена. Вважається, що елементи, що знаходяться в холодному резерві не відмовляють.
3 В полегшеному (теплом резерві), при якому резервна одиниця включена, але без навантаження, тобто надійність в резервному стані вище, ніж в робочому.
Оптимізація надійності ВС
На практиці при проектуванні складних систем виникає завдання створення такої системи, яка забезпечувала б максимальну або задану ефективну надійність. Показник якості функціонування складної системи покращують різними шляхами, в тому числі зміною структури і принципу її функціонування, а також за рахунок підвищення надійності елементів системи. У зв'язку з цим виникає завдання оптимального резервування системи.
Розглянемо її в такій постановці. Є складна багатофункціональна система, що складається з кінцевого безлічі елементів N, з'єднаних певним чином. Кожен елемент знаходиться або в стані відмови (позначимо його умовно xi = 0), або в стані працездатності (позначимо його через xi = 1). У довільний момент часу система опиняється в одному з 2 N різних станів х = [x1. x2, ..., xN].
Позначимо через P [y (i), x], приватну (умовну) ефективність системи (або якість виконання завдання), яка залежить від x. У свою чергу, розподіл x залежить від виду функції yi - розподілу резерву за елементами.
В якості критерію оцінки надійності складної системи вибирають ефективність в наступному вигляді:
де p (x) - ймовірність того, що система знаходиться в стані х.
Підсумовування проводиться по всіх x, що пробігає 2 N можливих значень.
Розглянемо постановку задачі в двох наступних формулюваннях:
А) Знайти такий закон розподілу обмежених коштів, при якому значення середньої ефективності системи (2.1) брало максимальне значення за умови, що
,
де y0 - задана надмірність системи.
С) Знайти такий закон розподілу мінімальних засобів, при якому значення середньої ефективності системи (2.1) досягло б заданої ефективності: