І саме в цей день, мені хочеться поділитися з усіма Вами відкриттями, які жодній людині не були доступні протягом багатьох і багатьох тисячоліть. І зовсім не важливо, що багато хто навіть не чули про їхнє існування. Важливий сам смисл. Хто має вуха - почує, хто має розум - зрозуміє.
Існує безліч способів і варіантів, за допомогою циркуля і лінійки без розмітки, розділити довільно взятий кут на три рівні частини. Мені відоме не менше трьох десятків, але системних рішень не так і багато: мені відомо - не більш семи. Кажу це не для додання ваги собі або своїм словам, бо те, про що сказано раніше, в доважком не потребує. Кажу це для тих, хто і зараз продовжує пошуки вирішення цього завдання. Продовжуйте шукати, і ви обов'язково знайдете.
Сьогодні ж, ми відкриємо для себе варіант рішення, який називається:
«Класичне рішення» поділу кута на три частини за допомогою циркуля і лінійки без розмітки.
Як ділити прямий, повний і розгорнутий кути все ми знаємо ще зі шкільної програми, тому сьогодні ми їх не розглядаємо.
Отже: завдання, таємниця тисячоліть -
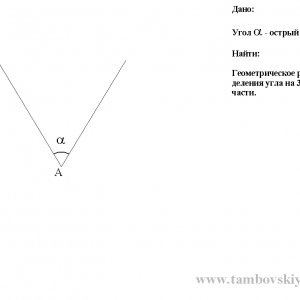
Знайти геометричне рішення поділу кута на 3 рівні частини.
Рішення буде дано універсальне для гострого, тупого і розгорнутого кутів одночасно базуються на одному кресленні.
1. З вершини гострого кута А довільним розчином циркуля накреслив коло n;
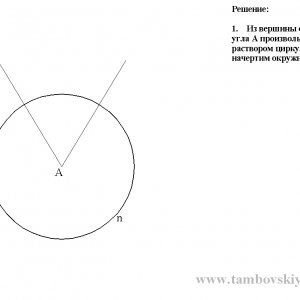
2. З'єднаємо прямий точки перетину променів кута А з окружністю n, отримаємо трикутник АВС;
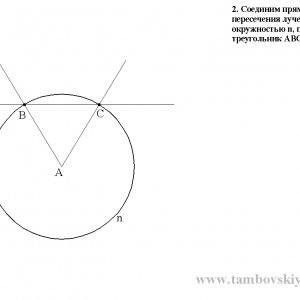
3. Розділимо кут А на 2 частини. Для цього з вершин В і С трикутника АВС накреслив дві дуги (до перетину) радіусом, рівним стороні трикутника; Проведемо пряму X через точки перетину дуг. Пряма розділить кут А на дві рівні частини, а також розділить на 2 частини окружність n. Точки перетину прямої X з окружністю n позначимо, як точка 1 і 2, а точку перетину прямої Х зі стороною трикутника, як точка 3;
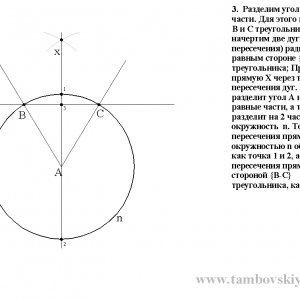
Що й треба було за умовою завдання для розгорнутого кута ВАС
Тут, ще раз доречно буде нагадати, що перевіряти правильність накреслення прямих ліній і кіл, а також точок перетинів їх, доцільніше після кожного, знову виробленого, геометричного дії. І, якщо принцип симетричності, принцип дзеркального відображення лівого правого, верхнього нижнього вам дотримати вдалося, то ви в одному кроці від позитивного результату рішення.
Ось і минула невизначеності.
Все таємне стає явним.
Час розкидати - і час збирати.
дружні сайти
