Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
§ 24. Рішення задач за допомогою лінійних рівнянь. Рівняння як математична модель задачі
Ми вже розглядали приклади функціональної залежності між величинами як математичні моделі реальних процесів. Тепер розглянемо текстові задачі, математичними моделями яких є лінійні рівняння і рівняння, що зводяться до лінійних.
Вирішувати завдання за допомогою рівняння слід в такій послідовності:
1) позначити змінної одну з невідомих величин;
2) інші невідомі величини (якщо вони є) висловити через введену змінну:
3) за умовою завдання встановити співвідношення між невідомими і відомими значеннями величин і скласти рівняння;
4) вирішити отримане рівняння;
5) проаналізувати рішення рівняння і знайти невідому величину, а при необхідності і значення інших невідомих величин;
6) записати відповідь до задачі.
Розглянемо кілька задач і вирішимо їх за допомогою лінійного рівняння.
Завдання 1. На свій день народження сестрички-близнючки Наталя і Олена отримали разом 127 вітальних SMS - повідомлень, причому Наталя отримала 13 повідомлень більше, ніж Олена. За скільки SMS-повідомлень на свій день народження отримала кожна з сестричок?
Рішення. Нехай Олена отримала х повідомлень, тоді Наталя - (х + 13). А обидві разом - (х + х + 13) повідомлень, що за умовою дорівнює 127.
Маємо рівняння: х + х + 13 = 127. Звідки х = 57.
Отже, Олена отримала 57 повідомлень,
57 + 13 = 70 (повідом.) - отримала Наталія.
В і д п о в е д ь: 70 повідомлень; 57 повідомлень.
Завдання 2. Максимально можлива сума кредиту розраховується банком за формулою:
де S - сума кредиту, С - середньомісячна зарплата позичальника. Для кредиту терміном в один рік вважають, що n = 9, терміном два роки - n = 21, терміном на три роки - n = 33. Якою має бути найменша середньомісячна зарплата позичальника, щоб банк падав йому кредит в сумі 30 000 грн на:
Р о з в 'я з а н н я. За умовою S = 30 000 грн. Нехай найменша середньомісячна зарплата позичальника становить х грн.
1) Чи маємо рівняння: 30 000 = ∙ 9; звідки х = 10 000.
Отже, середньомісячна зарплата позичальника повинна бути не менше 10 000 грн.
2) Чи маємо рівняння: 30 000 = ∙ 21; звідки х ≈ 4285,7.
Отже, середньомісячна зарплата повинна бути не менше 4286 грн.
3) Чи маємо рівняння: 30 000 = ∙ 33; звідки х ≈ 2727,3.
Отже, якщо позичальник хоче отримати кредит на три роки, то його середньомісячна зарплата повинна бути не менше 2728 грн.
В і д п о в е д ь: 1) 10 000 грн; 2) 4286 грн; 3) 2728 грн.
Завдання 3. З міста А до міста В. відстань між якими 310 км, виїхав вантажний автомобіль. Через 30 хв після цього з міста В в місто А виїхав легковий автомобіль, швидкість якого на 20 км / год більше швидкості вантажного. Автомобілі зустрітися через 2 години після виїзду легкового автомобіля. Знайти швидкість кожного автомобіля.
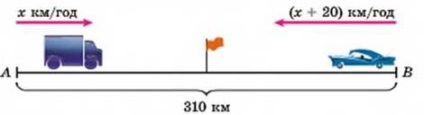
Р о з в 'я з а н н я. Нехай швидкість вантажного автомобіля - х км / год. Умова завдання зручно представити у вигляді таблиці:
Оскільки автомобілі виїхали в протилежних напрямках і зустрілися, то разом вони проїхали 310 км.
Маємо рівняння: 2, 5х + 2 (х + 20) = 310.
Вирішимо його: 2,5 х 2 х 40 = 310; 4,5 = 270;
х = 60 (км / год) - швидкість вантажного автомобіля;
60 + 20 - 80 (км / год) - швидкість легкового автомобіля.
Відповідь: 60 км / год; 80 км / год.
Якого порядку слід дотримуватися, вирішуючи завдання за допомогою рівняння?
892. (Усно) Одне число на 20 більше другого. Менше з них позначено через х. Висловіть через х більше з цих чисел.
893. (Усно) Одне позитивне число в 5 разів більше за друге. Менше з них позначено через х. Висловіть через х більше з цих чисел.
894. На одній клумбі росте х кущів троянд, а на другий - удвічі більше. Висловіть через х кількість кущів троянд, що ростуть на другий клумбі.
895. (Усно) Відстань, рівну х км велосипедист долає за 5 годин. Висловіть через х швидкість його руху.
896. (Усно) Перше число позначили через х, а друге становить чверть від першого. Висловіть друге число через х.
897. Перше число дорівнює х. а друге становить 70% від першого. Висловіть через х друге число.
898. (Усно) Сума довжин двох відрізків дорівнює 10 см. Довжина одного з інших см. Виразіть через х довжину другого відрізка.
899. (Усно) Власна швидкість човна дорівнює 18 км / год, а швидкість течії - х км / год. Висловіть через х швидкість човна за течією і проти течії.
900. Загадали число. Якщо від нього відняти 7 і отриманий результат розділити на 9, то отримаємо 12. Яке число загадали?
901. Знайдіть число, половина якого разом з його третин частиною дорівнює 40.
902. В двох цистернах разом 58 т палива, причому в першій на 4 т менше, ніж у другій. Скільки тонн пального в кожній цистерні?
903. В автопарку вантажних автомобілів в 6 разів більше, ніж легкових. Скільки легкових автомобілів в автопарку, якщо їх разом з вантажними 91?
904. Одне з двох позитивних чисел втричі більше другого. Знайдіть ці числа, якщо їх різниця дорівнює 28.
905. Бабусі разом з мамою 99 років. Скільки років кожної з них, якщо бабуся старше мами на 25 років?
906. Сума двох чисел 360, а їх відношення дорівнює 5. 7. Знайдіть ці числа.
907. Різниця двох чисел 42, а їх відношення дорівнює 7. 4. Знайдіть ці числа.
908. Периметр трикутника дорівнює 20 дм. Дві його сторони рівні між собою і кожна з них на 1 дм більше третьої. Знайдіть сторони трикутника.
909. За два дні було продано 384 кг бананів, причому другого дня продали від того, що продали першого. Скільки кілограмів бананів продали в перший день і скільки - в другій?
910. Туристи за другий день подолали від того відстані, яку подолали першого дня. Скільки кілометрів подолали туристи першого дня і скільки другого, якщо за перший день було подолано на 3 км більше, ніж за другий?
911. За пральну машину і її підключення заплатили 2940 грн. Вартість підключення становить 5% від вартості машина. Скільки коштує пральна машина?
912. Бабуся ліпила вареники протягом двох годин. За другу годину вона виліпила на 5% більше вареників, ніж за першу. Скільки вареників виготовила бабуся за першу годину і скільки за другу, якщо за другу годину вона виліпила на 3 вареники більше, ніж за першу?
913. За 2 год мотоцикліст долає таку ж відстань, що і велосипедист за 5 годин. Швидкість мотоцикліста на 27 км / год більше швидкості велосипедиста. Знайдіть швидкість кожного з них.
914. Ящик з апельсинами на 3 кг важчий, ніж ящик з лимонами. Яка маса кожного з них, якщо маса чотирьох ящиків з апельсинами така ж, як маса п'яти ящиків з лимонами?
915. З міста в село турист йшов зі швидкістю 4 км / год, а повертався назад зі швидкістю 3 км / год. На весь шлях він витратив 7 годин. Знайдіть відстань від міста до села.
916. Периметр прямокутника дорівнює 36 см, причому одна з його сторін на 4 см більша за іншу. Знайдіть сторони прямокутника і його площа.
918. У Маші було втричі більше грошей, ніж у Олі. Після того як Маша витратила 18 грн, грошей у дівчаток стало порівну. Скільки грошей мала кожна з дівчат спочатку?
919. Мережа кондитерських до річниці свого відкриття дарувала відвідувачам набори солодощів торгових марок «Добре», «Солодко» і «Смачно». В кінці святкування з'ясувалося, що наборів «Солодко» було подаровано на 12 більше, ніж наборів «Добре», а наборів «Смачно» - на 31 більше, ніж &всехuo;Солодко ». За скільки наборів кожної марки було подаровано, якщо відвідувачів було 430 і кожен з них отримав по одному набору?
920. Одна сторона трикутника на 9 см менше другий і вдвічі менше третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 105 см.
921. Можна розкласти 68 банок консервів в три ящика так, щоб у другому було вдвічі більше банок, ніж в першому, а в третьому - на 3 банки менше, ніж в першому?
922. Або можна 90 книг розмістити на трьох полицях так, щоб на третій було на 3 книги більше, ніж на другий, і на 5 книг менше, ніж на першій?
923. Батькові зараз - 38 років, а його синові - 10. Через скільки років батько буде втричі старше сина?
924. На одній ділянці кущів агрусу і втричі більше, ніж на другий. Якщо з першої ділянки пересадити 12 кущів на другий, то кущів агрусу на обох ділянках стане порівну. За скільки кущів агрусу зростає на кожній ділянці?
925. В двох корпусах пансіонату проживала однакову кількість відпочиваючих. У зв'язку з проведенням ремонту було вирішено переселити 24 відпочиваючі з першого корпусу до другого, після чого кількість відпочиваючих в першому корпусі стала в 4 рази менше, ніж у другому. За скільки відпочиваючих проживало в кожному корпусі до початку ремонтних робіт?
926. В двох мішках цукру було порівну. Після того як з першого мішка пересипали 8 кг до другого, в ньому стало вдвічі менше цукру, ніж у другому. За скільки кілограмів цукру було в кожному мішку спочатку?
927. На 33 гривні було придбано 24 зошити в лінійку і клітинку. Вартість зошити в лінійку - 1 грн 20 коп. а в клітинку - 1 грн 50 коп. За скільки зошитів кожного виду купили?
929. Старовинна грецька завдання. У Піфагора запитали: «Скільки учнів навчається в твоїй школі?». На що він відповів: «Половина всіх моїх учнів вивчає математику, чверть - музику, сьома частина мовчить, і, крім того, є ще три жінки». Скільки учнів навчалося в школі Піфагора?
930. Маса бідона з молоком становить 25 кг і ще половину його маси. Яка маса бідона з молоком?
931. від одного числа дорівнює - від другого. Знайдіть ці числа, якщо їх сума дорівнює 66.
932. 60% від одного числа рівні 45% від другого. Знайдіть ці числа, якщо їх сума дорівнює 210.
933. Човен витратив на шлях за течією 2,5 ч, а проти течії 3,6 годину. Відстань, яку проплив човен за течією, опинився на 7,6 км менше, ніж відстань, яке він проплив проти течії. Знайдіть власну швидкість човна, якщо швидкість течії дорівнює 2 км / год.
934. Катер за течією річки плив 1,6 год, а проти течії - 2,5 год. Відстань, яку подолав катер проти течії, виявилася па 6,2 км більше, ніж відстань, яку подолав катер за течією. Знайдіть швидкість течії, якщо власна швидкість катера дорівнює 16 км / год.
935. З пункту А до пункту В зі швидкістю 12 км / год виїхав велосипедист. Через 3 год з пункту В В пункт А виїхав мотоцикліст зі швидкістю 45 км / год. Скільки годин до зустрічі з мотоциклістом їхав велосипедист, якщо відстань від А до В становить 235,5 км? На якій відстані від пункту А сталася їхня зустріч?
936. З котеджного містечка в напрямку залізничної станції зі швидкістю 14 км / год виїхав велосипедист, а через 2 години після нього звідти ж, але в протилежному напрямку зі швидкістю 4 км / год вийшов пішохід. Через скільки годин після свого виходу пішохід буде на відстані 73 км від велосипедиста? На якій відстані від котеджного містечка в цей час він буде перебувати?
937. Один кавун на 5 кг легше другий і в три рази легше, ніж третій. Перший і третій кавуни разом в два рази важче другий. Знайдіть масу кожного кавуна.
938. Під час підготовки до олімпіади з математики Іван вирішив на 3 завдання менше, ніж Оксана, і в 2 рази менше, ніж Сергій. При цьому Іван і Сергій разом розв'язали в 2,1 рази більше завдань, ніж Оксана. Яка кількість завдань вирішив кожен учень, готуючись до олімпіади?
Вправи для повторення
5. Чи рівносильні рівняння 3х - 2 = х + 8 і 2 (х - 3) = х - 1?
6. В одному кошику було в два рази більше грибів, ніж у другому. За скільки грибів було в кожній кошику, якщо в обох кошиках разом було 78 грибів?
2) 5х - (х + 5) = 4 (х - 2).
8. Човен за течією плив 3,5 год, а проти течії - 4,2 год. Відстань, яку проплив човен за течією, опинився на 9,8 км більше, ніж відстань, яке він проплив проти течії. Знайдіть власну швидкість човна, якщо швидкість течії дорівнює 2 км / год.
9. Знайдіть всі цілі значення а, при яких корінь рівняння ах = -6 є цілим числом.
10. Розв'яжіть рівняння | 3 - 4-х | = 5.
11. З міста в село відправився пішохід зі швидкістю 4 км / год. Через 2 год з села в місто виїхав велосипедист зі швидкістю 16 км / год. Скільки годин до зустрічі з пішоходом їхав велосипедист, якщо відстань від села до міста становить 38 км?