У замкнутої (ізольованою від зовнішніх тіл) термодинамічної системи зміна внутрен-неї енергії будь-якого тіла системи # 916; U1 не може приводити до зміни внутрішньої енергії всієї системи. отже,
Якщо всередині системи не відбувається робота ніякими тілами, то, згідно з першим законом термодинаміки, зміна внутрішньої енергії будь-якого тіла відбувається тільки за рахунок обміну теплом з іншими тілами цієї системи: # 916; Ui = Qi. З огляду на. отримаємо:
,
Це рівняння називається рівнянням теплового балансу. Тут Qi - кількість теплоти, по-лучанин або віддане i -им тілом. Будь-яке з кількостей теплоти Qi може означати теплоту, що виділяється або поглинається при плавленні будь-якого тіла, згорянні палива, випаровуванні або конденсації пари, якщо такі процеси відбуваються з різними тілами системи, і будуть визначаться відповідними співвідношеннями.
Рівняння теплового балансу є математичним виразом закону збереження енер-гііпрі теплообміні.
Робота при розширенні газу
1 / V (див. Рівняння (4)). Зростаючи, газ виробляє роботу. Нехай в циліндрі поршень площею S під дією постійної сили F пересунувся внаслідок розширення газу на рассто-яние dx. Робота газу дорівнюватиме:
Якщо F змінюється, то: (21).
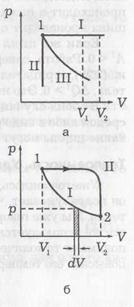
На ріс.б p # 903; dV - це площа заштрихованої смужки, a - це сума площ всіх смужок від V1 до V2. T. о. робота газу через міряється площею під кривою на діаграмі p -V. Очевидно, що ра-бота залежить від процесу, т. Е. Від того, чи відбувається розширення газу по кривій I або по кривій II (видно, що на рис. Б під кривою II площа більше, ніж під кривою I).
При ізобаріческом процесі (рис. А. Крива I) робота газу:
При ізохоричному процесі (рис. А. Крива II) обсяг не змінюється, т. Е. DV = 0 і, таким чи-тельно, А = 0. При ізотермічному процесі змінюються і р. і V (рис. б). Замінивши тиск через обсяг і температуру, відповідно до рівняння (4), отримаємо роботу газу при T = const:
Проведемо процес розширення газу зі стану 1 (рис. Б) в стан 2 по кривій II (А> 0), а стиснення назад в стан 1 - по кривій I (А<0 ). Процесс с возвращением в ту же точку называется цик-лом. Тогда общая работа будет равна разности площадей под кривыми II и I, т. е. пло-щади цикла.
Якщо цикл на діаграмах p -V відбувається за годинниковою стріл-ке (див. Рис. Б), то робота при розширенні більше, ніж при стисканні і повна робота А> 0. Оскільки ми повертаємося в ту ж точку, # 916; U = 0. З (18) випливає, що при такому процесі і теп-лота, що підводиться до тіла, повинна бути більше нуля (Q> 0). Так відбувається в тепловій машині, коли тепло підводиться, а ма-шина виробляє позитивну роботу.
Якщо ж цикл відбувається проти годинникової стрілки, то А <0. Соответственно и Q <0, т. е. энергия не подводится к телу, а отводится от него. Это имеет место в холодильнике.
В обох випадках відбувається обмін енергією з навколишнім середовищем або у вигляді роботи, або у вигляді обміну теплотою.
еплоемкость - це кількість теплоти, яку необхідно повідомити системі для збільшення її температури на 1 (К) при відсутності корисної роботи і сталості відповідних параметрів.
Якщо в якості системи ми беремо індивідуальна речовина, то загальна теплоємність системи дорівнює теплоємності 1 моль речовини () помножене на число моль ().
Теплоємність може бути питома і молярна.
Питома теплоємність - це кількість теплоти, необхідне для нагрівання одиниці маси речовини на 1 град (інтенсивна величина).
Молярна теплоємність - це кількість теплоти, необхідне для нагрівання одного моль речовини на 1 град.
Розрізняють справжню і середню теплоємність.
У техніці зазвичай використовують поняття середньої теплоємності.
Середня - це теплоємність для певного інтервалу температур.
Якщо системі, яка містить кількість речовини або масою. повідомили кількість теплоти. а температура системи підвищилася від до. то можна розрахувати середню питому або молярна теплоємність:
Справжня молярна теплоємність - це відношення нескінченно малої кількості теплоти, повідомленої 1 моль речовини при певній температурі, до приросту температури, яке при цьому спостерігається.
Відповідно до рівняння (19), теплоємність, як і теплота, не є функцією стану. При постійному тиску або обсязі, відповідно до рівнянь (11) і (12), теплота, а, отже, і теплоємність набувають властивостей функції стану, тобто стають характеристичними функціями системи. Таким чином, отримуємо ізохорно і ізобарну теплоємності.
Ізохорно теплоємність - кількість теплоти, яку необхідно повідомити системі, щоб підвищити температуру на 1. якщо процес відбувається при.
Ізобарна теплоємність - кількість теплоти, яку необхідно повідомити системі, щоб підвищити температуру на 1 при.
Теплоємність залежить не тільки від температури, але і від обсягу системи, оскільки між частинками існують сили взаємодії, які змінюються при зміні відстані між ними, тому в рівняннях (20) і (21) використовують приватні похідні.
Ентальпія ідеального газу, як і його внутрішня енергія, є функцією лише температури:
а відповідно до рівняння Менделєєва-Клапейрона. тоді
Тому для ідеального газу в рівняннях (20), (21) приватні похідні можна замінити на повні диференціали:
З спільного вирішення рівнянь (23) і (24) з урахуванням (22), отримаємо рівняння взаємозв'язку між і для ідеального газу.
Розділивши змінні в рівняннях (23) і (24), можна розрахувати зміна внутрішньої енергії та ентальпії при нагріванні 1 моль ідеального газу від температури до
Якщо в зазначеному інтервалі температур теплоємність можна вважати постійної, то в результаті інтегрування отримуємо:
Встановимо взаємозв'язок між середньою і істинної теплоємністю. Зміна ентропії з одного боку виражається рівнянням (27), з іншого -
Прирівнявши праві частини рівнянь і висловивши середню теплоємність, маємо:
Аналогічне вираз можна отримати для середньої ізохорно теплоємності.
Теплоємність більшості твердих, рідких і газоподібних речовин підвищується з ростом температури. Залежність теплоємності твердих, рідких і газоподібних речовин від температури виражається емпіричним рівнянням виду:
де а. b. c і - емпіричні коефіцієнти, обчислені на основі експериментальних даних про. причому коефіцієнт відноситься до органічних речовин, а - до неорганічних. Значення коефіцієнтів для різних речовин приведені в довіднику і застосовні тільки для зазначеного інтервалу температур.
Теплоємність ідеального газу не залежить від температури. Згідно молекулярно-кінетичної теорії теплоємність, яка припадає на одну ступінь свободи, дорівнює (ступінь свободи - число незалежних видів руху на які можна розкласти складний рух молекули). Для одноатомної молекули характерно поступальний рух, яке можна розкласти на три складові відповідно до трьох взаємно перпендикулярними напрямками по трьох осях. Тому ізохорно теплоємність одноатомного ідеального газу дорівнює
Тоді ізобарна теплоємність одноатомного ідеального газу згідно (25) визначиться з рівняння
Двоатомних молекули ідеального газу крім трьох ступенів свободи поступального руху мають і 2 ступеня свободи обертального руху. отже: