Безперервна випадкова величина, яка набуває значень, тільки належать відрізку [a. b] з постійною щільністю розподілу, називається розподіленої по рівномірному закону.
Функція щільності розподілу ймовірностей визначається співвідношенням
Знайдемо функцію розподілу даної випадкової величини:
Графіки функцій f (x) і F (x) зображені на малюнках 13 і 14.
Малюнок 13 - Графік функції f (x) рівномірного розподілу
Малюнок 14 - Графік функції F (x) рівномірного розподілу
Математичне сподівання випадкової величини X. розподіленої по рівномірному закону на ділянці [a. b], як випливає з механічною інтерпретації (центр маси), так само абсциссе середини ділянки: M [X] = (a + b) / 2. Цей же результат можна отримати і обчислюючи інтеграл:
Дисперсію випадкової величини X також можна знайти, виходячи з механічною інтерпретації (момент інерції розподілу щодо центру маси): D [X] = (b - a) 2/12. Той же результат можна отримати, обчислюючи інтеграл:
Середнє квадратичне відхилення рівномірно розподіленої випадкової величини
Моди рівномірний розподіл не має; його медіана з міркувань симетрії дорівнює (a + b) / 2. З тих же міркувань симетрії коефіцієнт асиметрії A [X] = 0. Коефіцієнт ексцесу випадкової величини X дорівнює -1,2: Ex [X] = -1,2; як і слід було очікувати, він від'ємний.
Прикладом випадкової величини, яка має рівномірний закон розподілу, є час очікування регулярних подій, наприклад, час очікування поїзда в метрополітені, час очікування автобуса визначеного маршруту на зупинці.
Розглянемо кілька прикладів випадкових величин, що мають рівномірний розподіл. При проведенні вимірювань деякої величини за допомогою приладу з великими розподілами помилки округлення розподілені по рівномірному закону. Очевидно, що рівномірний розподіл мають і помилки, що виникають від округлення даних при розрахунках.
Приклад 36 Потяги метрополітену йдуть з інтервалом в 4 хвилини. Пасажир приходить на платформу поїзди в довільний момент часу. Знайти ймовірність того, що він буде очікувати приходу поїзда не більше однієї хвилини. Знайти середній час очікування поїзда пасажиром, обчислити дисперсію і середнє квадратичне відхилення часу очікування поїзда пасажиром.
Рішення. Розглянемо випадкову величину X - час очікування пасажиром поїзда. Всі можливі значення даної випадкової величини належать відрізку [0; 4], і, згідно з умовою, всі ці значення рівноможливими. Отже, випадкова величина розподілена по рівномірному закону з параметрами a = 0 і b = 4. Функція щільності розподілу ймовірностей даної випадкової величини:
Знайдемо ймовірність того, що пасажир чекатиме потяг не більше однієї хвилини:
На малюнку 15 штрихуванням виділено фігура, площа якої дорівнює ймовірності
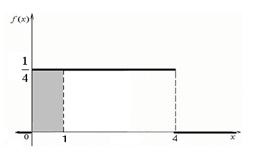
Малюнок 15 - Графік щільності розподілу ймовірностей
випадкової величини X - часу очікування пасажиром поїзда
Середній час очікування приходу поїзда пасажиром
Середнє квадратичне відхилення