коливальні системи, стан динамічний. системи, до-рої не змінюється в часі. Р. с. можуть бути стійкими, нестійкими і байдуже-стійкими. Рух системи поблизу положення рівноваги (при меншому від нього відхиленні) може бути істотно різними в залежності від характеру типу) Р. с.
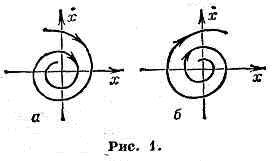
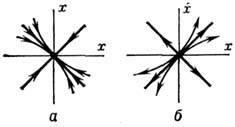
Для систем з одним ступенем свободи, якщо Р. с. стійко, при малому обуренні (відхиленні) система повертається до нього, здійснюючи затухаючі коливання (на фазової площині - (див. фазового простору) - такого руху відповідає стійкий фокус; рис 1, а), або аперіодично (стійкий вузол; рис. 2, а).
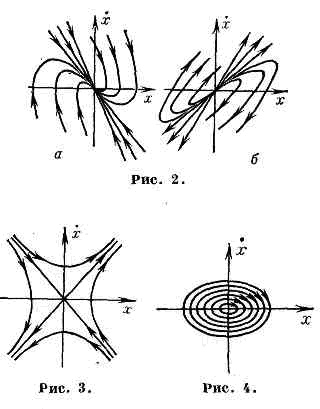
Поблизу нестійкого Р. с. малі відхилення наростають, здійснюючи коливання (нестійкий фокус; рис. 1, б), або аперіодично (нестійкий вузол; рис. 2, б); поблизу седлового Р. с. (Рис. 3) можливо спочатку наближення до Р. с. а потім догляд. Нарешті, в разі байдуже-стійкого Р. с. (Центр; рис. 4) малі відхилення призводять до незгасаючих коливань поблизу Р. с. Для систем з дек. ступенями свободи рух поблизу Р. с. може бути більш складним і істотно залежати від характеру поч. відхилення. Рух динамічний. системи поблизу Р. с. найчастіше описується лінеаризоване ур-нями, що мають рішення в вигляді суми експонент aelit з комплексними (у загальному випадку) типовий. показниками li. Р. с. стійко, якщо действит. частини всіх типовий. показників негативні (Reli 0) - рис. 2, фокус (Iml1,2? 0, Rel1 = Rel2? 0) - рис. 1, сідло (Iml1,2 = 0, Rel1 • Rel2
динамічної системи - стан динамічної системи, до-рої не змінюється в часі. Р. с. може бути стійким, нестійким і байдуже-стійким. Рух системи поблизу рівноваги (при меншому від нього відхиленні) істотно розрізняється залежно від характеру (типу) Р. с. У разі систем з одним ступенем свободи, якщо Р. с. стійко, то при малому обуренні (відхиленні) система повертається до нього, здійснюючи затухаючі коливання (на фазової площині такого руху відповідає стійкий фо-кус - рис. 1, а) або рухаючись аперіодично (стійкий вузол - рис. 2, а). Поблизу нестійкого Р. с. малі відхилення системи наростають, при цьому система здійснює коливання (нестійкий фокус - рис. 1, б) або рухається аперіодично (нестійкий вузол - рис. 2, б); поблизу седлового Р. с. (Рис. 3) можливо спочатку наближення до Р. с. а потім відхід від нього. Нарешті, в разі байдуже-стійкого Р. с. ( "Центр", рис. 4) малі відхилення призводять до незгасаючих коливань поблизу Р. с. Для систем з дек. ступенями свободи рух системи поблизу Р. с. може бути більш складним і істотно залежить від характеру початкового відхилення.
Мал. 1. Поведінка траєкторій в околиці стійкого (а) і нестійкого (б) фокусів; тут n = 2, =; а <0 ( а ) и а> 0 (б).
Мал. 2. Траєкторії в околиці стійкого (а) і нестійкого (б) вузлів; l2
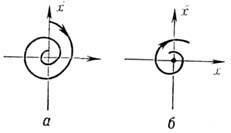
Мал. 3. Стан рівноваги типу "сідло".
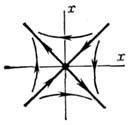
Мал. 4. Замкнуті траєкторії в околиці точки типу "центр".
Рух динамічний. системи поблизу Р. с. найчастіше описується лінеарізов. ур-нями, що мають рішення в вигляді сум експонент з комплексними (у загальному випадку) типовий. показниками li - корінням типовий. ур-ня: det (A -lE) = 0, де а Xi - права частина діфференц. ур-ний, що описують досліджувану систему:
х * - рішення, яке відповідає рівновазі, Х (х *) = 0. Якщо Relk <0 (Relk> 0), то Р. с. асимптотично стійко (нестійкий) і через всі крапки в околиці х * проходять траєкторії, які прагнуть до x * при t. (T. -,), - рис. 1.
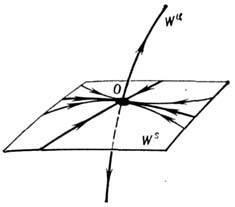
якщо Relk <0, k=1. т, Relk> 0, j = = т + 1. n. то Р. с.- "сідло"; траєкторії, які прагнуть до нього при t. (T. -,), лежать на стійкому (нестійкому) різноманітті - багатовимірної сепаратріси розмірності т (п - т) - рис. 5.
Мал. 5. "Сідло" в тривимірному фазовому просторі; l2 <
У консервативних (зокрема, гамільтонових) динамічний. системах стійкими (по Ляпунову) можуть бути лише Р. с. з чисто уявними або нульовими lk. Напр. незгасаючі коливання кульки в "потенційній ямі" (рис. 4) описуються рухом точки по замкнутої траєкторії в околиці Р. с. типу "центр", для к-якого
Якщо динамічний. система залежить від параметра, то (навіть і в неконсервативний випадку) при його зміні Relk може звернутися в нуль, і тоді Р. с. може зазнавати біфуркації, пов'язані з втратою (придбанням) стійкості або зі зміною розмірності його сепаратріси (див. також Стійкість руху).
Літ .: Андронов А. А. Вітт А. А. Хай, кін С. 9. Теорія коливань, 3 вид. М. 1981; Бау-тин Н. Н. Леонтович E. А. Методи і прийоми якісного дослідження динамічних систем на площині, М.,
1976; Арнольд В. І. Додаткові глави теорії звичайних диференціальних рівнянь, М. 1 978 ..
В. С. Афраймовіч, М. І. Рабинович.
Дивитися що таке "РІВНОВАГИ СТАН" в інших словниках:
СТАН - (1) аморфне (рентгеноаморфное) стан твердої речовини, в якому немає кристалічної структури (атоми і молекули розташовані безладно), воно изотропно, т. Е. Має однакові фіз. властивості в усіх напрямках і не має чіткої ... ... Велика політехнічна енциклопедія
СТАН метастабільних - нестійкий стан рівноваги, коли дана фаза може існувати необмежений час без зміни, але варто тільки в цій фазі з'явитися зародку інший, більш стійкою фази, як негайно настає перетворення. При цьому ... ... Геологічна енциклопедія
стан рівноваги - pusiausviroji būsena statusas T sritis fizika atitikmenys: angl. equilibrium state vok. Gleichgewichtszustand, m rus. рівноважний стан, n; стан рівноваги, n pranc. état d'équilibre, m ... Fizikos terminų žodynas
РІВНОВАГИ ПОЛОЖЕННЯ - системи звичайних диференціальних рівнянь (*) точка така, що х = xявляется (постійним за часом) рішенням системи (*); Р. п. Наз. також і саме це рішення. Точка є Р. п. Системи (*) тоді і тільки тоді, коли f (t, x) = 0 при всіх t. ... ... Математична енциклопедія
Метастабільні стани - стан нестійкої рівноваги фіз. системи, в до ром система може перебувати довгих. час, не переходячи в більш стійке (за даних умов) стан. Перехід в більш стійкий стан відбувається під дією зовн. факторів або ... ... Природознавство. енциклопедичний словник
КРИТИЧНЕ СТАН - стан, в до ром 2 разл. фази, що знаходяться між собою в рівновазі, стають тотожними по всьому св вам. К. с. може спостерігатися тільки в тих випадках, коли 2 співіснують фази якісно подібні, т. е. обидві ізотропні (рідина пар, ... ... Великий енциклопедичний політехнічний словник
Нерівноважногостану - стан термодинамич. системи, що характеризується неоднорідністю розподілу темп ри, тиску, щільності, концентрацій компонентів або к. л. ін. макроскопіч. параметрів під час відсутності зовн. полів або обертання системи як цілого. Неоднорідність ... Природознавство. енциклопедичний словник