Припустимо, що джерело випромінювання є дифузним подібно светодиоду і має випромінює площа. Інтенсивність випромінювання вважається постійною для всього світу, сколлімірованного лінзою передавача. Лінза має ефективну апертуру і фокусна відстань. Оптичний приймач розташований на відстані. Його ефективна апертура дорівнює і вважається, що весь падаючий на неї світло сфокусований на активній області фотодетектора. Для того щоб максимізувати прийняту потужність зображення джерела випромінювання має формуватися в площині приймальні апертури. Використовуючи елементарну теорію тонкої лінзи, можна знайти відстань від джерела випромінювання до центру лінзи передавача зі співвідношення:
а площа його зображення визначити за формулою:
Потужність випромінювання, зібраного лінзою передавача:
Вважаючи, що зображення джерела заповнює апертуру. частина потужності. яка досягає фотодетектора, просто дорівнює. так що приймається потужність:
де - енергетична яскравість джерела. Звідси ясно, що потрібно джерело випромінювання з високою енергетичною яскравістю і з апертурою більшої площі. Розглянемо як приклад систему, в якій використовується світлодіод з яскравістю, що має апертуру площею (діаметр 35 мм). На відстані в 1 км потужність падаючого на приймач випромінювання. Хоча, ці обчислення зроблені для ідеальної линзовой системи, основні висновки застосовні і в тому випадку, якщо використовуються дзеркальна або катадіоптричні (змішана дзеркальна і лінзова) системи для того, щоб коллімірованним і зібрати випромінювання. У будь-якому випадку через аберації зображення, сформовані в реальній оптичній системі, є недосконалими.
Рис.4.8. Радіальний розподіл густини потужності
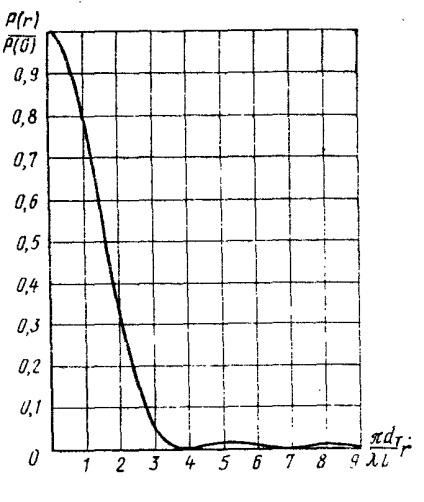
Якщо джерело занадто малий, то розмір його зображення не можна визначати за формулою (4.15), а слід шукати виходячи з дифракції світла на апертурі лінзи передавача. Добре відомо, що дифракційна картина, створювана однорідно освітленій круглою апертурою. складається з декількох концентричних кілець. Радіальне зміна щільності потужності приймає форму, показану на рис.4.8.
Можна сказати, що розмір зображення є дифракційно обмеженим, коли радіус першого мінімуму інтенсивності, або першого темного кільця дифракційної картини, стає порівнянним за величиною з діаметром добре сфокусованого зображення, тобто коли виконується співвідношення
де - діаметр джерела. звідси випливає
Світло від лазерного джерела, будучи за своєю природою високо коллімірованним і когерентним, зазвичай дає дифракційно-обмежене зображення джерела. У будь-якому випадку інтенсивність випромінювання в центрі дифракційної картини визначається виразом. де - загальна випромінювана потужність. У разі точкового джерела визначається за допомогою (4.16), а в інших випадках як площа апертури. Сумарна потужність випромінювання, що збирається невеликий приймальні апертурою площею. розташованої в центрі дифракційної картини, в загальному випадку визначається за формулою
а в разі точкового джерела з інтенсивністю випромінювання
Слід мати на увазі, що наведені формули дають завищені значення потужності і на практиці матимуть місце додаткові втрати в оптичній системі в результаті аберацій.
Розглянемо обставини при яких описана вище оптична система зв'язку, яка використовує світлодіод (), може стати дифракційно-обмеженою. Припустимо що і фокусна відстань лінзи передавача. У цьому випадку зі співвідношення випливає, що дифракція визначатиме розбіжність пучка тільки тоді, коли діаметр джерела. Таким чином, світлодіод з торцевих випромінюванням забезпечить виконання умови дифракційно-обмеженої системи, а з випромінюючої поверхнею - немає.
Для зменшення дифракційної расходимости лазерного джерела випромінювання можна використовувати розширювач пучка (рис.4.9).
Рис.4.9. Розширювач пучка, який використовується, для зменшення його розбіжність, обумовленої дифракцією
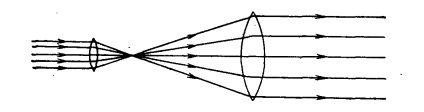
В результаті апертура, на якій відбувається дифракція, збільшується. Як приклад припустимо, що випромінювання напівпровідникового лазера потужністю 10 мВт колімуючих і заповнює об'єктив розширювача пучка діаметром 10мм. Тоді, прийнявши, як і раніше, і знаходимо, що потужність на відстані
Якщо розбіжність пучка настільки мала, що не перевищує 0,1мрад, то необхідна точність наведення буде пред'являти жорсткі вимоги до системи управління променем і механічної стабільності будь-якого портативного передавача.
Вирази (4.20) і (4.21) справедливі при однорідному освітленні передавальної апертури. Інший випадок, в якому обумовлене дифракцией розподіл потужності в дальній зоні можна легко обчислити, має місце, коли щільність потужності в ближній зоні приймає гауссова розподіл, як показано на рис.4.10. На практиці це важливо, тому що відповідно до теорії основна поперечна мода випромінювання лазера циліндричним резонатором дає саме такий розподіл вихідної потужності, і це спостерігається в дійсності.
Цю систему найкраще описати за допомогою циліндричних координат з початком в центрі падаючої апертури. Будемо припускати радіальну сіссетрію і, таким чином, ігнорувати азимутально координату. Нехай розподіл щільності потужності в ближній зоні передавальної апертури має вигляд:
Тоді в площині (за умови, що) розподіл щільності потужності
Якщо приймальня апертура настільки мала (, що експоненціальне член всюди приблизно дорівнює одиниці, то приймається потужність
Легко показати, що загальна випромінювана потужність
Що ідентично висловом (4.20), якщо ми розглядаємо, як ефективну площу передавальної апертури.
Характеристики спрямованості антенних систем описується наступним чином. Якби не використання великої апертури передавача. то потужність джерела випромінювалася б рівномірно у всіх напрямках. На відстані вона розподілилася б на площі. Основний приймач з узгодженою, зовсім не спрямованої антеною забезпечує приймається випромінювання ефективну площу апертури, рівну. Тоді основні втрати при передачі та є частиною изотропно випромінюваної потужності, яка могла б бути прийнята основним приймачем. Зазвичай втрати виражаються в децибелах. Якщо для концентрації переданого пучка використовується спрямована антенна решітка з великою апертурою, то інтенсивність дифракційно обмеженого пучка максимально зростає в раз. Величина відома як «коефіцієнт посилення» антени приймача. Ці співвідношення виявляють існування принципу оборотності між антенами приймача і передавача, що обгрунтовано, коли мова йде про радіочастоти. Однак вони не мають місця на практиці в оптичному діапазоні. Загальні втрати при передачі
Або з урахуванням (4.20)
Якщо. . і. основні втрати при передачі становить. коефіцієнт посилення антени передавача. коефіцієнт посилення антени приймача. що дає загальні втрати при передачі [13].