У даній статті розглядаються принципи розрахунку балок рівного опору вигинає моменту, тобто таких балок прямокутного перерізу, один з геометричних параметрів поперечного перерізу яких зменшується обернено пропорційно до чинного вигинає моменту. Основні принципи розрахунку таких балок такі ж, як і балок рівного опору вигинає моменту, але є деякі особливості.
1. Розрахунок балок прямокутного перерізу, зміна одного з геометричних параметрів перетину якої носить зворотний характер, може виконуватися на підставі наступних припущень:
1.1. Так як ні один з геометричних параметрів, наприклад, ширина шарнірно опертої балки змінюватися від b на початку прольоту, до 0 в середині прольоту не може (така балка зруйнується), то спочатку виконується розрахунок по міцності і виходячи з цього розрахунку визначаються геометричні параметри найбільш навантаженого перетину. Отже таку балку можна розглядати як дві балки: одну з постійною шириною, а другу з шириною змінюється від δb до 0. При цьому епюра моментів характеризує прогин для балки постійного перетину, а крім того цю епюру можна розглядати, як епюру нормальних напружень для балки постійного перетину.
1.2. Загальна епюра нормальних напружень, що виникають в поперечних перетинах балки, характеризує загальний прогин балки.
1.3 Якщо накласти епюру моментів на епюру напружень балки змінного перерізу, то дотриманні певних умов різниця між цими епюрами покаже зміна прогину для балки змінного перерізу.
Точніше різниця площ цих епюр можна розглядати як якусь фіктивну навантаження і тоді різниця цих епюр покаже зміна фіктивної опорної реакції А, а при розподілі отриманого значення на жорсткість - зміна кута повороту на опорі А. Тоді фіктивний момент (фіктивна опорна реакція, помножена на відстань від точки прикладання фіктивної опорної реакції до розглянутої точки, мінус площа разностной епюри, помножена на відстань від центру ваги разностной епюри до розглянутої точки) покаже зміна прогину.
Примітка. принципи графоаналітичного методу в даній статті на розглядаються.
Наприклад, для балки з лінійно змінюється шириною b разностная епюра буде виглядати так:
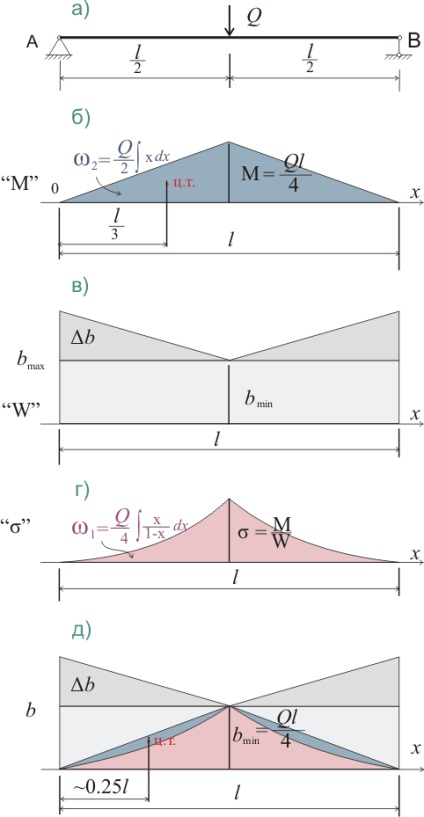
При цьому на разностную епюру буде впливати не тільки характер навантаження на балку, але також і величина відхилення від мінімально допустимого розміру поперечного перерізу. Так, якщо δb → 0, то перетин балки прагне до постійного значення. При значному збільшенні δb в порівнянні з b зменшується ефективність використання матеріалу, хоча при цьому і прогин зменшується. Умова δb → b не допускається прийнятими в п.1.1 обмеженнями. Тому розрахунок балок з перетином, що зменшується від початку балки до середини, залежить від значення bmin. Крім того, від значень bmin і δb залежить характер зміни нормальних напружень.
Прогин балки з лінійно зменшується шириною перетину при зосередженому навантаженні посередині прольоту
1.4. Так як зміна нормальних напружень для балки з зосередженим навантаженням описується залежністю виду:
то при постійному значенні h 2/6 = C = 1 формула (323.1.1) набуде вигляду:
Після відповідних перетворень отримаємо наступну залежність:
Де bmin в даному випадку постійна величина і її значення також можна прийняти рівним 1. Тоді наприклад, при δb = bmin = b / 2, n = 2, у = 2х, разностная епюра описується двома лініями, які мають таку залежність:
В даному випадку значення опорної реакції А = Q / 2 - постійна величина і для спрощення розрахунків її можна винести за межі інтегрування. Дані лінії перетинаються в точках 0 і 0.5 (початок балки і середина прольоту або нижня і верхня межа інтегрування), тоді:
тоді площа разностной епюри складе:
Примітка. В даному випадку нас цікавить разностная епюра тому, що визначити відстань до центра ваги разностной епюри набагато простіше, ніж шукати центр ваги для епюри з площею ω1. Візуально (ріс.323.1 д) ця відстань складає l / 4. Крім того для візуальної оцінки результатів інтегрування для епюр моментів і напруг на малюнках 323.1 - 323.3 спочатку будувалися графіки функцій (див. Ріс.323.1.2).
Значення фіктивного згинального моменту складе:
Mф = Ql 2/16 (l / 3) - (0.22712Ql 2/16) (l / 4) = Ql 3/48 - 0.17Ql 3/48 = 0.83Ql 3/48 (323.2.5)
У даній випадку Ibmin означає, що ми розглядаємо зміну прогину по відношенню до балки з постійним моментом інерції і відповідно постійної шириною перетину bmin.
Щоб було ще більш наочно, для розглянутого випадку збільшення матеріалу балки в 1.5 рази призводить до зменшення прогину в 1.184 рази.
Якщо зміна ширини перерізу буде описуватися іншою залежністю, то наближені результати можна отримати інтерполяцією даних малюнка 323.1.2.
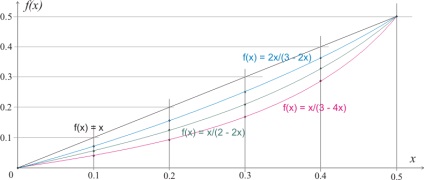
Як видно з даного малюнка, при співвідношенні δb / b = 1/3 (f (x) = 2x / (3 - 2x)) площа разностной епюри буде приблизно в 2 рази менше, ніж при розглядався співвідношенні 1/2. При співвідношенні 2/3 площа разностной епюри збільшиться приблизно на 1/2.
Прогин балки з лінійно зменшується шириною перетину при рівномірно розподіленому навантаженні
При рівномірно розподіленим навантаженням зміниться і епюра моментів і епюра нормальних напружень
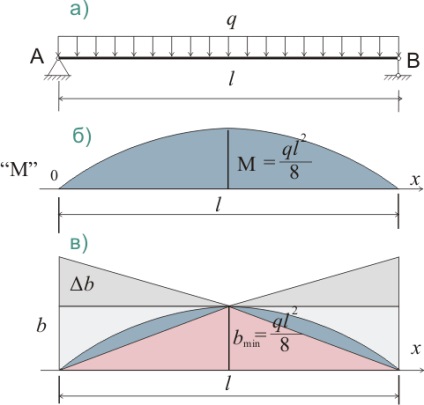
σ = М / W = 6 (qlx - qx 2) / 2bh 2 (323.4.1)
то при постійному значенні h 2/3 = C = 1 формула 323.1.1) набуде вигляду:
При bmin; = 1, при δb = bmin = b / 2, n = 2, у = 2х, разностная епюра описується двома лініями, які мають таку залежність:
Дані лінії перетинаються в точках 0 і 0.5 (початок балки і середина прольоту або нижня і верхня межа інтегрування), тоді:
тоді площа разностной епюри складе:
Тоді значення фіктивного згинального моменту складе:
Mф = ql 3/24 (5l / 16) - (ql 3/96) (l / 4) = 5ql 4/384 - ql 4/384 = ql 4/96 = 4ql 4/384 (323.4.8)
У даній випадку Ibmin також означає, що ми розглядаємо зміну прогину по відношенню до балки з постійним моментом інерції і відповідно постійної шириною перетину bmin.
Щоб було ще більш наочно, при рівномірно розподіленому навантаженні збільшення матеріалу балки в 1.5 рази призводить до зменшення прогину в 1.2 рази.
Якщо довжину балки також прийняти за якусь одиницю, що допустимо при обраних нами межах інтегрування, то рівняння функцій будуть виглядати так:
Тобто в даному випадку графік, що описує епюру напружень, має лінійну залежність (ріс.323.2 в).
Прогин балки з лінійно зменшується висотою при зосередженому навантаженні посередині балки
Так як момент опору W = bh 2/6 для прямокутного перерізу, то навіть при лінійно зменшується висоті залежність між нормальними напруженнями і епюр моментів буде не лінійною навіть при зосередженому навантаженні, прикладеної посередині балки. При рівномірно розподіленим навантаженням визначення прогину методом інтегрування ще більш ускладниться. Але в цілому вплив зміни висоти на прогин зміниться, так як в даному випадку слід розглядати не змінюється висоту, а квадрат змінюється висоти, а так як момент інерції це I = bh 3/12 для прямокутного перерізу, то епюру моментів слід порівнювати з кубічним зміною висоти перетину.
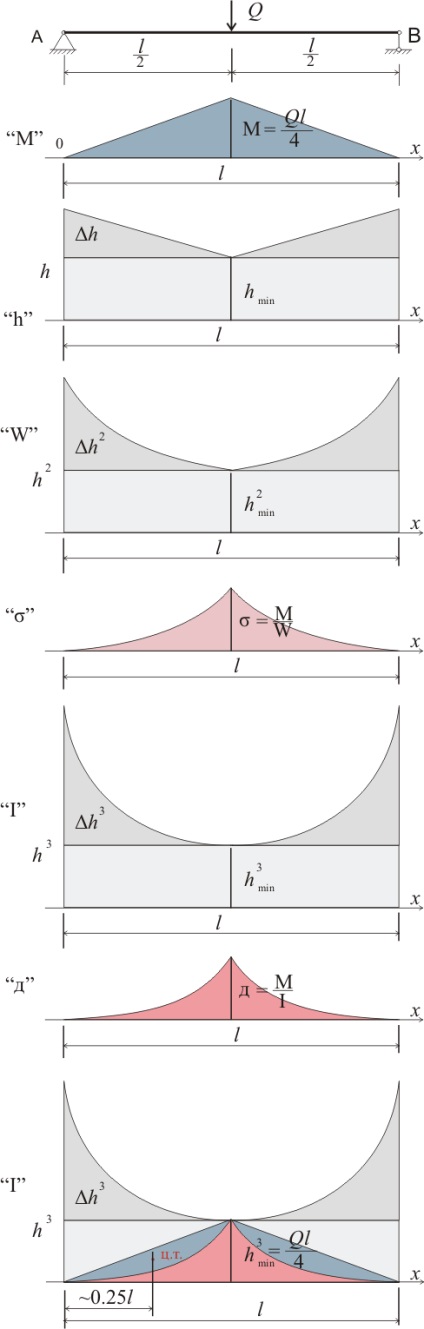
При δh = hmin = h / 2, n = 2, у = 2х, разностная епюра описується двома лініями, які мають таку залежність:
тоді площа разностной епюри складе:
Значення фіктивного згинального моменту складе:
Mф = Ql 2/16 (l / 3) - Ql 2/32 (l / 4) = Ql 3/48 - Ql 3/128 = (1 - 0.375) Ql 3/48 = 0.625Ql 3/48 (323.5. 5)
Примітка. відстань від центра ваги разностной епюри до початку координат визначено візуально за малюнком 323.3.
Прогин балки з лінійно зменшується висотою перетину при рівномірно розподіленому навантаженні
Так як при лінійно зменшується ширині перетину різниця в прогинах при зосередженому навантаженні, прикладеної посередині прольоту і рівномірно розподіленим навантаженням вкрай незначна, то можна припустити, що така ж незначна різниця буде і при лінійно змінюється висоті перетину. Тоді при δh = hmin = h / 2
Прогин балки з висотою перетину, зменшується пропорційно вигинає моменту
Прикладом такої балки є будь-яка шарнірно оперта залізобетонна балка з тріщинами в розтягнутій зоні. В результаті дії нормальних напружень висота стиснутої зони перерізу балки змінюється нелінійно. Цю залежність можна приблизно висловити так:
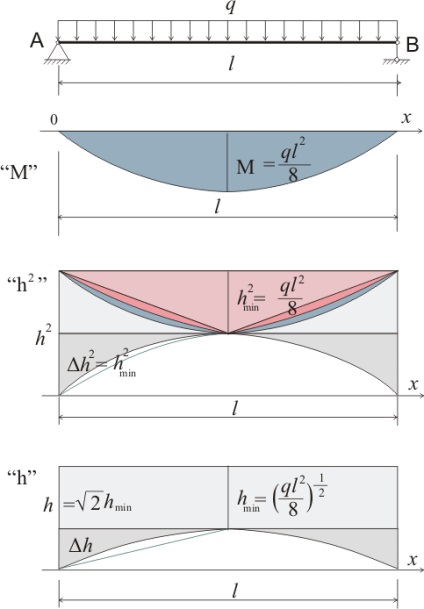
Залізобетонна балка з арматурою в розтягнутій зоні може розглядатися як балка змінного перерізу. У поперечних перетинах, в яких вигинає момент дорівнює нулю або дуже малий, що стискають напруги викликають пружні деформації бетону, що розтягують напруги викликають пружні деформації і бетону і арматури. При обраної розрахункової схемою сжимаемой буде верхня частина розтину, а розтягується нижня частина перетину. Після того, як розтягують напруги досягнуть межі міцності бетону при розтягуванні, бетон в розтягується зоні почне руйнуватися - почнуть утворюватися тріщини - і тому з збільшенням напруг, що розтягують все більшу частину цих напруг буде сприймати арматура і все меншу частину бетон нижній частині перетину. Таким чином буде зменшуватися висота приведеного перерізу балки. Мінімальною висота приведеного перерізу буде в точці дії максимального згинального моменту.
При цьому збільшення згинального моменту буде приводити до зменшення квадрата висоти стиснутої зони перетину (епюра "h 2"). На епюрі "h 2" також показано вплив нелінійної зміни висоти перетину в порівнянні з лінійним зміною висоти перетину. При подібному нелінійному зміні висоти площа разностной епюри при співвідношенні hmin = h / 2 буде в 2 рази менше, ніж при лінійному зміні висоти.
Якщо розглядати тільки пружні деформації стиснутої області поперечних перерізів бетону, то зменшення квадрата висоти в два рази означає зміну висоти δh від 0 до hmin / √ 2.
Таким чином, використовуючи дані, отримані при розгляді балок з лінійно зменшується шириною і висотою перетину, сумарний вплив нелінійної зміни висоти і зміни співвідношення hmin / h можна висловити так:
fпр ≈ 5ql 4 / 384EIhmin - 2ql 4 /(384·2·1.41EIhmin) = (5 - 0.7) ql 4 / 384EIhmin ≈ 4.3ql 4 / 384EIhmin ≈ 0.86 · 5ql 4 / 384EIhmin (323.7.6.1)
При цьому 0.86 можна розглядати як значення поправочного коефіцієнта, що враховує мінливу висоту балки.
Примітка. Більш точне визначення впливу змінюється висоти стиснутої зони перетину на прогин є досить трудомістким завданням, зокрема слід врахувати що висота перерізу почне змінюватися не відразу від початку балки, так як біля опор при даній розрахунковій схемі будуть ділянки без тріщин. Але навіть якщо в ході логічних міркувань були допущені помилки, то все одно точне значення коефіцієнта не може виходити за межі 0.8-0.9, тому для оціночних розрахунків прогину залізобетонних балок при рівномірно розподілених навантаженнях можна використовувати вказане у формулі (323.7.6) значення. Втім, на визначення прогину залізобетонних балок куди більший вплив можуть надати пластичні деформації в стислій зоні бетону і як наслідок - зменшення початкового модуля пружності бетону на деякій ділянці довжини балки, що можна розглядати і як додаткове зменшення висоти перетину.
Відповідно, якщо з яких-небудь причин зміна висоти перетину складе h / 2, то
fпр ≈ 5ql 4 / 384EIhmin - 2ql 4 / (384 · 2 · EIhmin) = (5 - 1) ql 4 / 384EIhmin ≈ 4ql 4 / 384EIhmin ≈ 0.8 · 5ql 4 / 384EIhmin (323.7.6.2)
Якщо зміна висот буде від 0 до hmin / 2√ 2. то
fпр ≈ 5ql 4 / 384EIhmin - 2ql 4 /(384·2·2·1.41EIhmin) = (5 - 0.35) ql 4 / 384EIhmin ≈ 4.65ql 4 / 384EIhmin ≈ 0.93 · 5ql 4 / 384EIhmin (323.7.6.3)