Тоді можна вивести формулу для i-го члена ряду:.
перший доданок (одиницю) винесли за суму, так як воно не відповідає загальній формулі, а c 1 = -1 / (3 # 8729; 4), c2 = 1 / (5 # 8729; 6) і т.д. Знак доданка отриманий за допомогою зведення -1 в ступінь, пропорційну номеру, тому змінюється на кожному кроці.
Відзначимо, що якщо пронумерувати члени суми, починаючи з номера 2, то формула для доданка буде простіше:
Ряд є нескінченним, а комп'ютер ж може підсумовувати лише кінцеве число доданків, інакше цикл вийде нескінченною. В цьому випадку можна або заздалегідь вибрати число доданків N, або (як потрібно в даному завданні) підсумовувати до досягнення заданої точності. Зазвичай вважається, що точність досягнута, якщо чергове доданок по модулю стало менше заданої точності | сi | Завдання знаходження суми ряду із заданою точністю може бути запрограмована за допомогою циклу з перед- або постусловіем. У наведеній програмі точність e позначена як eps. змінна z містить знак чергового доданка. Змінюючи його на кожному кроці в програмі простіше, ніж зводити в будь-яку ступінь (-1). read (eps); <ввод точности расчета> until abs (c) Введемо eps = 0.04. Другий доданок по модулю стає менше eps. При цьому s = 1-1 / (3 # 8729; 4) + 1 / (5 # 8729; 6) = 0,950. У разі необхідної точності 10 -6 результат s = 0,93883 при 500 доданків. Завдання 3.3.5: Обчислимо суму n доданків ряду із заданою точністю. У цьому завданню обчислювати чергове доданок через його номер не дуже зручно, так як кожен раз потрібно заново розраховувати значення факторіала. З іншого боку, легко бачити, що черговий член ряду можна отримати з попереднього. Такі формули називаються рекурентними. Якщо взяти перший доданок С1 = x 3/2. то С2 = С1 * х 3/3, С3 = С2 * х 3/4, і так далі. Суму ряду з точністю eps можна порахувати за допомогою наведеної нижче програми. Звертаємо увагу читачів на те, що не потрібно в циклі повторювати те, що обчислюється за все один раз. Наприклад, якщо в попередньому прикладі обчислити х 3 до циклу. то програма буде ефективніше і швидше працювати. Даний ряд буде обов'язково сходитися при будь-якому x, тому що факторіал зростає швидше статечної функції. Перевірити правильність обчислень окремих доданків можна, поставивши всередину циклу оператор, який виведе на екран значення доданків і суми на кожному кроці, наприклад для даного завдання writeln (i: 5: 0, c: 8: 4, s: 10: 5); після обчислення змінних з і s. Наприклад, при точності eps = 0.01 і x = 2. Результат роботи програми буде наступний.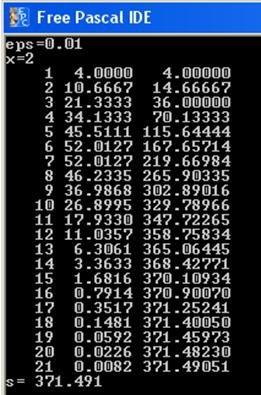
Схожі статті